JEE Main Mathematics Permutations and Combinations Online Test
Finish Quiz
0 of 30 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
Information
JEE Main Mathematics Permutations and Combinations Online Test. JEE Main Online Test for Mathematics Permutations and Combinations. JEE Main Full Online Quiz for Mathematics Permutations and Combinations. JEE Main Free Mock Test Paper 2021. JEE Main 2021 Free Online Practice Test, Take JEE Online Test for All Subjects. JEE Main Question and Answers for Mathematics Permutations and Combinations. In this test You may find JEE Main all subjects Questions with Answers. Check JEE Main Question and Answers in English. This mock Test is free for All Students. Mock Test Papers are very helpful for Exam Purpose, by using below Mock Test Paper you may Test your Study for Next Upcoming Exams. Now Scroll down below n Take JEE Main Mathematics Permutations and Combinations…
This paper has 30 questions.
Time allowed is 30 minutes.
The JEE Main Mathematics Permutations and Combinations is Very helpful for all students. Now Scroll down below n click on “Start Quiz” or “Start Test” and Test yourself.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 30 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Answered
- Review
-
Question 1 of 30
1. Question
How many 5-digit telephone numbers can be constructed using the digits 0 to 9, if each number starts with 67 and no digit appears more than once?
Correct
Number of ways to fill the IIIrd place = 8
Number of ways to fill the IVth place = 7
Number of ways to fill the Vth place = 6
Hence, by FPC total number of ways = 8 × 7 × 6 = 56 × 6 = 336
Incorrect
Number of ways to fill the IIIrd place = 8
Number of ways to fill the IVth place = 7
Number of ways to fill the Vth place = 6
Hence, by FPC total number of ways = 8 × 7 × 6 = 56 × 6 = 336
-
Question 2 of 30
2. Question
If the number of ways of selecting n cards out of unlimited number of cards bearing the number 0, 9, 3, so that they cannot be used to write the number 903 is 93, then n is equal to
Correct
We cannot write 903
If in the selection of n cards, we get either
(9 or 3), (9 or 0), (0 or 3), (only 0), (only 3) or (only 9)
Can be selected = 2 × 2 × 2 × ……… n times = 2n
Similarly, (9 or 0) or (3 or 0) can be selected 2n
In the above selection (only 0) or (only 3) or (only 9) is repeated twice
∴ Total ways = 2n + 2n + 2n – 3 = 93
⇒ 3.2n = 96
⇒ 2n = 32 = 25
∴ n = 5
Incorrect
We cannot write 903
If in the selection of n cards, we get either
(9 or 3), (9 or 0), (0 or 3), (only 0), (only 3) or (only 9)
Can be selected = 2 × 2 × 2 × ……… n times = 2n
Similarly, (9 or 0) or (3 or 0) can be selected 2n
In the above selection (only 0) or (only 3) or (only 9) is repeated twice
∴ Total ways = 2n + 2n + 2n – 3 = 93
⇒ 3.2n = 96
⇒ 2n = 32 = 25
∴ n = 5
-
Question 3 of 30
3. Question
Total number of works formed by using 2 vowels and 3 consonants taken from 4 vowels and 5 consonants is equal to
Correct
4C2 × 5C3 × 5! = 7200
Incorrect
4C2 × 5C3 × 5! = 7200
-
Question 4 of 30
4. Question
In a shelf there are 5 physics, 4 mathematics and 3 chemistry books. How many combinations are there if books of same subject are different
Correct
25 × 24 × 23 – 1 = 212 – 1 = 4095
Incorrect
25 × 24 × 23 – 1 = 212 – 1 = 4095
-
Question 5 of 30
5. Question
Find the number of different words that can be formed from the letters of the word TRIANGLE, so that no vowels are together.
Correct
In a word TRIANGLE, vowels are (A,E, I) and consonants are (G, L, N, R, T).
First, we fix the 5 consonants in alternate position in 5! ways.
_G_L_N_R_T_
In rest of the six blank positions, three vowels can be arranged in 6P3 ways.
∴ Total number of different words = 5! × 6P3
= 120 × 6 × 5 × 4 = 14400
Incorrect
In a word TRIANGLE, vowels are (A,E, I) and consonants are (G, L, N, R, T).
First, we fix the 5 consonants in alternate position in 5! ways.
_G_L_N_R_T_
In rest of the six blank positions, three vowels can be arranged in 6P3 ways.
∴ Total number of different words = 5! × 6P3
= 120 × 6 × 5 × 4 = 14400
-
Question 6 of 30
6. Question
If the letters of the word KRISNA are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word KRISNA is
Correct
The number of words starting from A are 5! = 120
The number of words starting from 1 are = 5! = 120
The number of words starting from KA are = 4! = 24
The number of words starting from KI are = 4! = 24
The number of words starting from KN are 4! = 24
The number of words starting from KRA are = 3! = 6
The number of words starting from KRIA are 2! = 2
The number of words starting from KRIN are = 2! = 2
The number of words starting from KRISA are = 1! = 1
The number of words starting from KRISNA are = 1! = 1
Hence, rank of the word KRISNA
= 2(120) + 3 (24) + 6 + 2(24) + 6 + 2(2) + (1) = 324
Incorrect
The number of words starting from A are 5! = 120
The number of words starting from 1 are = 5! = 120
The number of words starting from KA are = 4! = 24
The number of words starting from KI are = 4! = 24
The number of words starting from KN are 4! = 24
The number of words starting from KRA are = 3! = 6
The number of words starting from KRIA are 2! = 2
The number of words starting from KRIN are = 2! = 2
The number of words starting from KRISA are = 1! = 1
The number of words starting from KRISNA are = 1! = 1
Hence, rank of the word KRISNA
= 2(120) + 3 (24) + 6 + 2(24) + 6 + 2(2) + (1) = 324
-
Question 7 of 30
7. Question
The number of divisors of 9600 including 1 and 9600 are
Correct
9600 = 27 × 3 × 52
∴ No. of divisors = (7 + 1) × (1 + 1) × (2 + 1) = 8 × 2 × 3 = 48
Incorrect
9600 = 27 × 3 × 52
∴ No. of divisors = (7 + 1) × (1 + 1) × (2 + 1) = 8 × 2 × 3 = 48
-
Question 8 of 30
8. Question
Every one of the 10 available lamps can be switched on to illuminate certain Hall. The total number of ways in which the hall can be illuminated, is
Correct
210 – 1 = 1023
Incorrect
210 – 1 = 1023
-
Question 9 of 30
9. Question
How many numbers lying between 10 and 1000 can be formed from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 (repetition of digits is allowed)?
Correct
Case I when number of two digits.
Total number of ways = 9C1 × 9C1 = 9 × 9 = 81
Case II when number in three digits
Total number of ways = 9C1 × 9C1 × 9C1 = 9 × 9 × 9 = 729
∴ Total number of ways = 81 + 729 = 810
Incorrect
Case I when number of two digits.
Total number of ways = 9C1 × 9C1 = 9 × 9 = 81
Case II when number in three digits
Total number of ways = 9C1 × 9C1 × 9C1 = 9 × 9 × 9 = 729
∴ Total number of ways = 81 + 729 = 810
-
Question 10 of 30
10. Question
The number of diagonals that can be drawn in an octagon is
Correct
8C2 –8 = 28 – 8 = 20
Incorrect
8C2 –8 = 28 – 8 = 20
-
Question 11 of 30
11. Question
The number of ways in which a team of eleven players can be selected from 22 players always including 2 of them and excluding 4 of them is
Correct
∴ Required number of ways = 22–4–2C11–2 = 16C9
Incorrect
∴ Required number of ways = 22–4–2C11–2 = 16C9
-
Question 12 of 30
12. Question
Three boys of class X, four boys of class XI and five boys of class XII sit in a row. The total number of ways in which these boys can sit together is equal to
Correct
We can think of three packets. One consisting of three boys of class X, other consisting of four boys of class XI and last one consisting of five boys of class XII. These packets can be arranged in 3! ways and contents of these packets can be further arranged in 3!4! and 5! ways, respectively. Hence, the total number of ways is 3! × 3! × 4! × 5!
Incorrect
We can think of three packets. One consisting of three boys of class X, other consisting of four boys of class XI and last one consisting of five boys of class XII. These packets can be arranged in 3! ways and contents of these packets can be further arranged in 3!4! and 5! ways, respectively. Hence, the total number of ways is 3! × 3! × 4! × 5!
-
Question 13 of 30
13. Question
The total number of seven digit numbers the sum of whose digits is even, is
Correct
Suppose a1a2a3a4a5a6a7 represents a seven digit number. Then a1 takes the value 1, 2, 3, …… , 9 and a2,a3, ….. , a7 all take values 0, 1, 2, 3, …., 9. If we keep a1a2a3 …. a6 fixed, then the sum a1 +a2 + a3 + … …. + a6 is either even or odd. Since a7 takes 10 values 0, 1, 2, ……, 9 five of the numbers so formed will be even and five odd.
Hence, the required number of numbers
= 9∙10 ∙10 ∙10∙10∙10∙5 = 45 × 105
Incorrect
Suppose a1a2a3a4a5a6a7 represents a seven digit number. Then a1 takes the value 1, 2, 3, …… , 9 and a2,a3, ….. , a7 all take values 0, 1, 2, 3, …., 9. If we keep a1a2a3 …. a6 fixed, then the sum a1 +a2 + a3 + … …. + a6 is either even or odd. Since a7 takes 10 values 0, 1, 2, ……, 9 five of the numbers so formed will be even and five odd.
Hence, the required number of numbers
= 9∙10 ∙10 ∙10∙10∙10∙5 = 45 × 105
-
Question 14 of 30
14. Question
The sum of the digits in unit place of all the numbers formed with the help of 3, 4, 5 and 6 taken all at a time is
Correct
The sum of the digit in unit place of all the numbers formed = 3! (3 + 4 + 5 + 6) = 6 × 18
= 108
Incorrect
The sum of the digit in unit place of all the numbers formed = 3! (3 + 4 + 5 + 6) = 6 × 18
= 108
-
Question 15 of 30
15. Question
An n digit number is a positive number with exactly n digits. Nine hundred distinct n digit numbers are to be formed using only the three digits 2, 5 and 7. The smallest value of n for which this is possible is
Correct
Each place can be filled in 3 ways
∴ n places can be filled in 3n
∴ 3n ≥ 900
∴ 36 = 729 and 37 = 2187
Hence n = 7
Incorrect
Each place can be filled in 3 ways
∴ n places can be filled in 3n
∴ 3n ≥ 900
∴ 36 = 729 and 37 = 2187
Hence n = 7
-
Question 16 of 30
16. Question
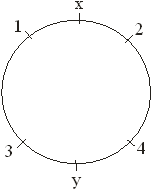
Three boys and three girls are to be seated around a table, in a circle. Among them the boy x does not want any girl neighbor and the girl y does not want any boy neighbor. The number of such arrangement is
Correct
x, 1, 2, are boys and y, 3, 4 are girls
No. of arrangement = 2! × 2! = 4
Incorrect
x, 1, 2, are boys and y, 3, 4 are girls
No. of arrangement = 2! × 2! = 4
-
Question 17 of 30
17. Question
The number of ways in which we can choose a committee from four men and six women so that the committee includes at least two men and exactly twice as many women as men is
Correct
The number of ways in which we can choose a committee
= Choose two men and four women + choose three men and six women
= 4C2 ×6C4 + 4C3 × 6C6
= 6 × 15 + 4 × 1 = 90 + 4 = 94
Incorrect
The number of ways in which we can choose a committee
= Choose two men and four women + choose three men and six women
= 4C2 ×6C4 + 4C3 × 6C6
= 6 × 15 + 4 × 1 = 90 + 4 = 94
-
Question 18 of 30
18. Question
A question paper is divided into two parts A and B and each part contains 5 questions. The number of ways in which a candidate can answer 6 questions selecting at least two questions from each part is
Correct
The number of ways that the candidate may select
(i) if 2 questions from A and 4 questions from B = 5C2 × 5C4 = 50
(ii) 3 questions from A and 3 questions from B = 5C2 × 5C3 = 100
and (iii) 4 questions from A and 2 questions from B = 5C4 × 5C2 = 50
Hence, total number of ways = 50 + 100 + 50 = 200
Incorrect
The number of ways that the candidate may select
(i) if 2 questions from A and 4 questions from B = 5C2 × 5C4 = 50
(ii) 3 questions from A and 3 questions from B = 5C2 × 5C3 = 100
and (iii) 4 questions from A and 2 questions from B = 5C4 × 5C2 = 50
Hence, total number of ways = 50 + 100 + 50 = 200
-
Question 19 of 30
19. Question
No. of ways of arranging exactly 4 fruits from 5 apples, 4 mangoes and 2 oranges.
Correct
Coeff. of x4 in : (1 + x + x2 + x3 + x4 + x5) (1 + x +x2 + x3 +x4) (1 +x + x2)
: (1–x6) (1 –x5) (1–x3) (1–x)–3
: [1–x3] [1 – x]–3
: [3+4–1C4 – 3+4–1C1]
: 15 – 3
: 12
Incorrect
Coeff. of x4 in : (1 + x + x2 + x3 + x4 + x5) (1 + x +x2 + x3 +x4) (1 +x + x2)
: (1–x6) (1 –x5) (1–x3) (1–x)–3
: [1–x3] [1 – x]–3
: [3+4–1C4 – 3+4–1C1]
: 15 – 3
: 12
-
Question 20 of 30
20. Question
In an steamer, there are stalls for 12 animals and there are horses, cows and calves (not less than 12 each) ready to be shipped in how many ways can the ship load be made?
Correct
First stall can be filled in 3 ways, second stall can be filled in 3 ways and so on.
∴ Number of ways of loading steamer
= 3C1 × 3C1× …..×3C1 (12 times)
= 3 × 3 × ……× 3 (12 times) = 312
Incorrect
First stall can be filled in 3 ways, second stall can be filled in 3 ways and so on.
∴ Number of ways of loading steamer
= 3C1 × 3C1× …..×3C1 (12 times)
= 3 × 3 × ……× 3 (12 times) = 312
-
Question 21 of 30
21. Question
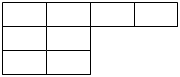
The number of different ways the letters of the word VECTOR can be placed in the 8 boxes of the given below such that no row empty is equal to
Correct
Total ways = (8C2 –2) × ⌊6
= (28 – 2) × ⌊6
= 26 × ⌊6
Incorrect
Total ways = (8C2 –2) × ⌊6
= (28 – 2) × ⌊6
= 26 × ⌊6
-
Question 22 of 30
22. Question
The prime ministers of 9 countries meet to discuss the terrorism problem. The number of ways they can seat themselves at a round table so that the Pakistan and India prime ministers sit together is (Pearson)
Correct
Treat India and Pakistan prime ministers as one (I, P) + 7 others we have to arrange 8 person round a table no. of ways = 7! but corresponding to each arrangement India and Pakistan prime ministers total way = 7!.2!
Incorrect
Treat India and Pakistan prime ministers as one (I, P) + 7 others we have to arrange 8 person round a table no. of ways = 7! but corresponding to each arrangement India and Pakistan prime ministers total way = 7!.2!
-
Question 23 of 30
23. Question
The number of mappings (functions) from the set A = {1, 2, 3} into the set B = {1, 2, 3, 4, 5, 6, 7} such thatf(i) < f(j), whenever i < j, is
Correct
If the function is one one, then select any three from the set B in 7C3 ways i.e., 35 ways.
If the function is many one, then there are two possibilities, All three corresponds to same element number of such functions = 7C1 = 7 ways. Two corresponds to same element. Select any two from the set B. The larger one corresponds to the larger and the smaller one corresponds to the smaller the third may corresponds to any two. Number of such functions = 7C2 × 2 = 42
So, the required number of mapping = 354 + 7 + 42 = 84
Incorrect
If the function is one one, then select any three from the set B in 7C3 ways i.e., 35 ways.
If the function is many one, then there are two possibilities, All three corresponds to same element number of such functions = 7C1 = 7 ways. Two corresponds to same element. Select any two from the set B. The larger one corresponds to the larger and the smaller one corresponds to the smaller the third may corresponds to any two. Number of such functions = 7C2 × 2 = 42
So, the required number of mapping = 354 + 7 + 42 = 84
-
Question 24 of 30
24. Question
The letter of the word RANDOM are written in all possible orders and these words are written out as in a dictionary. Then the rank of the work RANDOM is
Correct
Words beginning with A, D, M, N and O are 5! each. Words beginning with RAD are 3! and also for RAM are 3!. Then comes RAND. First we shall have RANDMO and the RANDOM.
∴ rank is 5(5!) + 2(3!) + 2 = 614
Incorrect
Words beginning with A, D, M, N and O are 5! each. Words beginning with RAD are 3! and also for RAM are 3!. Then comes RAND. First we shall have RANDMO and the RANDOM.
∴ rank is 5(5!) + 2(3!) + 2 = 614
-
Question 25 of 30
25. Question
Six points in a plane be joined in all possible ways by indefinite straight lines and if no two of them be coincident or parallel and no three pass through the same point (with the exception of the original 6 points). The number of distinct points or intersection is equal to
Correct
Number of lines from 6 point = 6C2 = 15
Points of intersection obtained from these lines = 15C2 = 105
Now, we find the number of times, the original 6 points come.
Consider one point say A1. Joining A1 to remaining 5 points, we get 5 lines and any two lines from these 5 lines gives A1 as the point of intersection.
∴ A1 is common in 5C2 = 10 times out of 105 points of intersections.
Similar is the case with other five points.
∴ 6 original points come 6 × 10 = 60 times in points of intersection.
Hence, the number of distinct points of intersection
= 105 – 60 + 6 = 51
Incorrect
Number of lines from 6 point = 6C2 = 15
Points of intersection obtained from these lines = 15C2 = 105
Now, we find the number of times, the original 6 points come.
Consider one point say A1. Joining A1 to remaining 5 points, we get 5 lines and any two lines from these 5 lines gives A1 as the point of intersection.
∴ A1 is common in 5C2 = 10 times out of 105 points of intersections.
Similar is the case with other five points.
∴ 6 original points come 6 × 10 = 60 times in points of intersection.
Hence, the number of distinct points of intersection
= 105 – 60 + 6 = 51
-
Question 26 of 30
26. Question
Six persons A, B, C, D, E and F are to be seated at a circular table. The number of ways this can be done if A must have either B or C on his right and B must have either C or D on his right is
Correct
Case-I If B is right on A
Sub case –I C is right on B
then no. of ways = (4 – 2)! = 6
Sub case-II if D is right on B
then no. of ways = (4 – 1)! = 6
Case-II if C is right on A
⇒ D must be right on B = (4 – 1)! = 3! = 6
Hence total no. of ways is 6 + 6 + 6 = 18
Incorrect
Case-I If B is right on A
Sub case –I C is right on B
then no. of ways = (4 – 2)! = 6
Sub case-II if D is right on B
then no. of ways = (4 – 1)! = 6
Case-II if C is right on A
⇒ D must be right on B = (4 – 1)! = 3! = 6
Hence total no. of ways is 6 + 6 + 6 = 18
-
Question 27 of 30
27. Question
If 5 parallel straight lines are intersected by 4 parallel straight lines, then the number of parallelograms, thus formed, is
Correct
Number of parallelograms = 5C2 × 4C2 = 60
Incorrect
Number of parallelograms = 5C2 × 4C2 = 60
-
Question 28 of 30
28. Question
The straight lines I1, I2, I3 are parallel and lie in the same plane. A total numbers of m points are taken on I1. n points on I2, k points on I3. The maximum number of triangles formed with vertices at these points is
Correct
Total number of points are m + n + k, the triangles formed by these points = m + n +kC3
Joining of three points on the same line gives no triangle, the number of such triangles is mC3 + nC3 + kC3
∴ Required number of triangles = m + n + kC3 – mC3 – nC3 – kC3
Incorrect
Total number of points are m + n + k, the triangles formed by these points = m + n +kC3
Joining of three points on the same line gives no triangle, the number of such triangles is mC3 + nC3 + kC3
∴ Required number of triangles = m + n + kC3 – mC3 – nC3 – kC3
-
Question 29 of 30
29. Question
In an examination there are three multiple choice questions and each question has 4 choices. Number of ways in which a student can fail to get all answers correct, is
Correct
Each question can be answered in 4 ways and all question can be answered correctly in only one way.
So, required number of ways = 63
Incorrect
Each question can be answered in 4 ways and all question can be answered correctly in only one way.
So, required number of ways = 63
-
Question 30 of 30
30. Question
Two straight lines intersect at a point R. Points P1, P2 ……….Pn are taken on one line and points Q1, Q2…..Qn on the other. If the point R is not be used, the number of triangles that can be drawn using these points as vertices, is
Correct
Incorrect