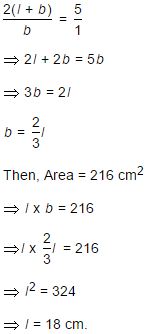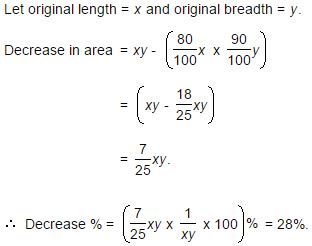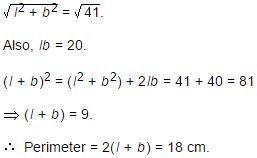Aptitude Area Online Test, Free Aptitude Quiz
Finish Quiz
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Aptitude Area Online Test, Free Aptitude Quiz, Online Aptitude Area Test. Aptitude Area Question and Answers 2021. Aptitude Area Quiz. Aptitude Area Free Mock Test 2021. Aptitude Area Question and Answers in PDF. The Aptitude Area online mock test paper is free for all students.The below Aptitude questions and answers can improve your skills in order to face the Interview, Competitive examination, Govt Exams and various entrance test with full confidence. Aptitude online test is very useful for exam preparation and getting for Rank. Aptitude Area Question and Answers in Hindi and English. Aptitude Area Mock test for topic via Online Mode. Here we are providing Aptitude Area Mock Test in Hindi. Now Test your self for “Aptitude Area Online Test in Hindi” Exam by using below quiz…
This paper has 20 questions.
Time allowed is 30 minutes.
The Aptitude Area online Mock Test is Very helpful for all students. Now Scroll down below n click on “Start Quiz” or “Start Test” and Test yourself.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
-
Question 1 of 20
1. Question
The ratio between the length and the breadth of a rectangular park is 3 : 2. If a man cycling along the boundary of the park at the speed of 12 km/hr completes one round in 8 minutes, then the area of the park (in sq. m) is:
Correct
Perimeter = Distance covered in 8 min. = (12000/60 × 8) m = 1600 m.
Let length = 3x metres and breadth = 2x metres.
Then, 2(3x + 2x) = 1600 or x = 160.
∴ Length = 480 m and Breadth = 320 m.
∴ Area = (480 × 320) m2 = 153600 m2.Incorrect
Perimeter = Distance covered in 8 min. = (12000/60 × 8) m = 1600 m.
Let length = 3x metres and breadth = 2x metres.
Then, 2(3x + 2x) = 1600 or x = 160.
∴ Length = 480 m and Breadth = 320 m.
∴ Area = (480 × 320) m2 = 153600 m2. -
Question 2 of 20
2. Question
An error 2% in excess is made while measuring the side of a square. The percentage of error in the calculated area of the square is:
Correct
100 cm is read as 102 cm.
∴ A1 = (100 x 100) cm2 and A2 (102 x 102) cm2.
(A2 – A1) = [(102)2 – (100)2]
= (102 + 100) x (102 – 100)
= 404 cm2.
∴ Percentage error = (404/100×100 × 100)x % = 4.04%Incorrect
100 cm is read as 102 cm.
∴ A1 = (100 x 100) cm2 and A2 (102 x 102) cm2.
(A2 – A1) = [(102)2 – (100)2]
= (102 + 100) x (102 – 100)
= 404 cm2.
∴ Percentage error = (404/100×100 × 100)x % = 4.04% -
Question 3 of 20
3. Question
The ratio between the perimeter and the breadth of a rectangle is 5 : 1. If the area of the rectangle is 216 sq. cm, what is the length of the rectangle?
Correct
Incorrect
-
Question 4 of 20
4. Question
The percentage increase in the area of a rectangle, if each of its sides is increased by 20% is:
Correct
Incorrect
-
Question 5 of 20
5. Question
A rectangular park 60 m long and 40 m wide has two concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109 sq. m, then what is the width of the road?
Correct
Area of the park = (60 x 40) m2 = 2400 m2.
Area of the lawn = 2109 m2.
∴ Area of the crossroads = (2400 – 2109) m2 = 291 m2.
Let the width of the road be x metres. Then,
60x + 40x – x2 = 291
⇒ x2 – 100x + 291 = 0
⇒ (x – 97)(x – 3) = 0
⇒ x = 3.Incorrect
Area of the park = (60 x 40) m2 = 2400 m2.
Area of the lawn = 2109 m2.
∴ Area of the crossroads = (2400 – 2109) m2 = 291 m2.
Let the width of the road be x metres. Then,
60x + 40x – x2 = 291
⇒ x2 – 100x + 291 = 0
⇒ (x – 97)(x – 3) = 0
⇒ x = 3. -
Question 6 of 20
6. Question
The diagonal of the floor of a rectangular closet is 7.5 feet. The shorter side of the closet is 4.5 feet. What is the area of the closet in square feet?
Correct
Incorrect
-
Question 7 of 20
7. Question
A towel, when bleached, was found to have lost 20% of its length and 10% of its breadth. The percentage of decrease in area is:
Correct
Incorrect
-
Question 8 of 20
8. Question
A man walked diagonally across a square lot. Approximately, what was the percent saved by not walking along the edges?
Correct
Incorrect
-
Question 9 of 20
9. Question
The diagonal of a rectangle is √41 cm and its area is 20 sq. cm. The perimeter of the rectangle must be:
Correct
Incorrect
-
Question 10 of 20
10. Question
What is the least number of squares tiles required to pave the floor of a room 15 m 17 cm long and 9 m 2 cm broad?
Correct
Length of largest tile = H.C.F. of 1517 cm and 902 cm = 41 cm.
Area of each tile = (41 × 41) cm2.
Required number of tiles = (1517 × 902/41 × 41) = 814.Incorrect
Length of largest tile = H.C.F. of 1517 cm and 902 cm = 41 cm.
Area of each tile = (41 × 41) cm2.
Required number of tiles = (1517 × 902/41 × 41) = 814. -
Question 11 of 20
11. Question
The difference between the length and breadth of a rectangle is 23 m. If its perimeter is 206 m, then its area is:
Correct
We have: (l – b) = 23 and 2(l + b) = 206 or (l + b) = 103.
Solving the two equations, we get: l = 63 and b = 40.
∴ Area = (l x b) = (63 x 40) m2 = 2520 m2.Incorrect
We have: (l – b) = 23 and 2(l + b) = 206 or (l + b) = 103.
Solving the two equations, we get: l = 63 and b = 40.
∴ Area = (l x b) = (63 x 40) m2 = 2520 m2. -
Question 12 of 20
12. Question
The length of a rectangle is halved, while its breadth is tripled. What is the percentage change in area?
Correct
Let original length = x and original breadth = y.
Original area = xy.
New length = x/2 .
New breadth = 3y.
New area = (x/2 × 3y) = 3/2 xy.
∴ Increase % = (1/2 xy × 1/xy × 100) % = 50%.Incorrect
Let original length = x and original breadth = y.
Original area = xy.
New length = x/2 .
New breadth = 3y.
New area = (x/2 × 3y) = 3/2 xy.
∴ Increase % = (1/2 xy × 1/xy × 100) % = 50%. -
Question 13 of 20
13. Question
The length of a rectangular plot is 20 metres more than its breadth. If the cost of fencing the plot @ 26.50 per metre is Rs. 5300, what is the length of the plot in metres?
Correct
Let breadth = x metres.
Then, length = (x + 20) metres.
Perimeter = (5300/26.50) m = 200 m.
∴ 2[(x + 20) + x] = 200
⇒ 2x + 20 = 100
⇒ 2x = 80
⇒ x = 40.
Hence, length = x + 20 = 60 m.Incorrect
Let breadth = x metres.
Then, length = (x + 20) metres.
Perimeter = (5300/26.50) m = 200 m.
∴ 2[(x + 20) + x] = 200
⇒ 2x + 20 = 100
⇒ 2x = 80
⇒ x = 40.
Hence, length = x + 20 = 60 m. -
Question 14 of 20
14. Question
A rectangular field is to be fenced on three sides leaving a side of 20 feet uncovered. If the area of the field is 680 sq. feet, how many feet of fencing will be required?
Correct
We have: l = 20 ft and lb = 680 sq. ft.
So, b = 34 ft.
∴ Length of fencing = (l + 2b) = (20 + 68) ft = 88 ft.Incorrect
We have: l = 20 ft and lb = 680 sq. ft.
So, b = 34 ft.
∴ Length of fencing = (l + 2b) = (20 + 68) ft = 88 ft. -
Question 15 of 20
15. Question
A tank is 25 m long, 12 m wide and 6 m deep. The cost of plastering its walls and bottom at 75 paise per sq. m, is:
Correct
Area to be plastered = [2(l + b) × h] + (l × b)
= {[2(25 + 12) × 6] + (25 × 12)} m2
= (444 + 300) m2
= 744 m2.
∴ Cost of plastering = Rs. (744 × 75/100) = Rs. 558.Incorrect
Area to be plastered = [2(l + b) × h] + (l × b)
= {[2(25 + 12) × 6] + (25 × 12)} m2
= (444 + 300) m2
= 744 m2.
∴ Cost of plastering = Rs. (744 × 75/100) = Rs. 558. -
Question 16 of 20
16. Question
Each of the questions given below consists of a question followed by three statements. You have to study the question and the statements and decide which of the statement(s) is/are necessary to answer the question.
What is the area of the hall?
I. Material cost of flooring per square metre is Rs. 2.50
II. Labour cost of flooring the hall is Rs. 3500
III. Total cost of flooring the hall is Rs. 14,500.Correct
I. Material cost = Rs. 2.50 per m2
II. Labour cost = Rs. 3500.
III. Total cost = Rs. 14,500.
Let the area be A sq. metres.
∴ Material cost = Rs. (14500 – 3500) = Rs. 11,000.
∴ 5A/2 = 11000 ⇔ A = 11000 × 2/5 = 4400 m2.
Thus, all I, II and III are needed to get the answer.
∴ Correct answer is (C).Incorrect
I. Material cost = Rs. 2.50 per m2
II. Labour cost = Rs. 3500.
III. Total cost = Rs. 14,500.
Let the area be A sq. metres.
∴ Material cost = Rs. (14500 – 3500) = Rs. 11,000.
∴ 5A/2 = 11000 ⇔ A = 11000 × 2/5 = 4400 m2.
Thus, all I, II and III are needed to get the answer.
∴ Correct answer is (C). -
Question 17 of 20
17. Question
Each of the questions given below consists of a question followed by three statements. You have to study the question and the statements and decide which of the statement(s) is/are necessary to answer the question.
What is the area of a right-angled triangle?
I. The perimeter of the triangle is 30 cm.
II. The ratio between the base and the height of the triangle is 5 : 12.
III. The area of the triangle is equal to the area of a rectangle of length 10 cm.Correct
From II, base : height = 5 : 12.
Let base = 5x and height = 12x.
Then, hypotenuse = √(5x)2 + (12x)2 = 13x.
From I, perimeter of the triangle = 30 cm.
∴ 5x + 12x + 13x = 30 ⇔ x = 1.
So, base = 5x = 5 cm, height = 12x = 12 cm.
∴ Area = (1/2 x 5 x 12)cm2 = 30 cm2.
Thus, I and II together give the answer.
Clearly III is redundant, since the breadth of the rectangle is not given.
∴ Correct answer is (A).Incorrect
From II, base : height = 5 : 12.
Let base = 5x and height = 12x.
Then, hypotenuse = √(5x)2 + (12x)2 = 13x.
From I, perimeter of the triangle = 30 cm.
∴ 5x + 12x + 13x = 30 ⇔ x = 1.
So, base = 5x = 5 cm, height = 12x = 12 cm.
∴ Area = (1/2 x 5 x 12)cm2 = 30 cm2.
Thus, I and II together give the answer.
Clearly III is redundant, since the breadth of the rectangle is not given.
∴ Correct answer is (A). -
Question 18 of 20
18. Question
Each of the questions given below consists of a question followed by three statements. You have to study the question and the statements and decide which of the statement(s) is/are necessary to answer the question.
What is the area of rectangular field?
I. The perimeter of the field is 110 metres.
II. The length is 5 metres more than the width.
III. The ratio between length and width is 6 : 5 respectively.Correct
I. 2(l + b) = 110 ⇒ l + b = 55.
II. l = (b + 5) ⇒ l – b = 5.
III. l/b = 6/5 ⇒ 5l – 6b = 0.
These are three equations in l and b. We may solve them pairwise.
∴ Any two of the three will give the answer.
∴ Correct answer is (B).Incorrect
I. 2(l + b) = 110 ⇒ l + b = 55.
II. l = (b + 5) ⇒ l – b = 5.
III. l/b = 6/5 ⇒ 5l – 6b = 0.
These are three equations in l and b. We may solve them pairwise.
∴ Any two of the three will give the answer.
∴ Correct answer is (B). -
Question 19 of 20
19. Question
Each of these questions is followed by three statements. You have to study the question and all the three statements given to decide whether any information provided in the statement(s) is redundant and can be dispensed with while answering the given question.
What is the area of the given rectangle?
I. Perimeter of the rectangle is 60 cm.
II. Breadth of the rectangle is 12 cm.
III. Sum of two adjacent sides is 30 cm.Correct
From I and II, we can find the length and breadth of the rectangle and therefore the area can be obtained.
So, III is redundant.
Also, from II and III, we can find the length and breadth and therefore the area can be obtained.
So, I is redundant.
∴ Correct answer is “II and either I or III”.Incorrect
From I and II, we can find the length and breadth of the rectangle and therefore the area can be obtained.
So, III is redundant.
Also, from II and III, we can find the length and breadth and therefore the area can be obtained.
So, I is redundant.
∴ Correct answer is “II and either I or III”. -
Question 20 of 20
20. Question
Each of these questions is followed by three statements. You have to study the question and all the three statements given to decide whether any information provided in the statement(s) is redundant and can be dispensed with while answering the given question.
What is the cost painting the two adjacent walls of a hall at Rs. 5 per m2 which has no windows or doors?
I. The area of the hall is 24 sq. m.
II. The breadth, length and height of the hall are in the ratio of 4 : 6 : 5 respectively.
III. Area of one wall is 30 sq. m.Correct
From II, let l = 4x, b = 6x and h = 5x.
Then, area of the hall = (24x2) m2.
From I. Area of the hall = 24 m2.
From II and I, we get 24x2 = 24 ⇔ x = 1.
∴ l = 4 m, b = 6 and h = 5 m.
Thus, area of two adjacent walls = [(l x h) + (b x h)] m2 can be found out and so the cost of painting two adjacent walls may be found out.
Thus, III is redundant.
∴ Correct answer is (C).Incorrect
From II, let l = 4x, b = 6x and h = 5x.
Then, area of the hall = (24x2) m2.
From I. Area of the hall = 24 m2.
From II and I, we get 24x2 = 24 ⇔ x = 1.
∴ l = 4 m, b = 6 and h = 5 m.
Thus, area of two adjacent walls = [(l x h) + (b x h)] m2 can be found out and so the cost of painting two adjacent walls may be found out.
Thus, III is redundant.
∴ Correct answer is (C).