CAT Online Test Series 1, CAT Free Mock Test | Free CAT Quiz
Finish Quiz
0 of 50 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
Information
CAT Online Test in English Series 1, CAT Free Mock Test Series 1. Common Admission Test (CAT) is one of the most challenging and competitive MBA entrance test in our country. Check your level of preparation for CAT with free All India Mock test 2021. RRB Exam Online Test 2021, CAT Free Mock Test Exam 2021. CAT Exam Free Online Quiz 2021, CAT Full Online Mock Test Series 1st in English. RRB Online Test for All Subjects, CAT Free Mock Test Series in English. CAT Free Mock Test Series 1. CAT English Language Online Test in English Series 1st. Here we are providing CAT Full Mock Test Paper in English. CAT Mock Test Series 1st 2021. Now Test your self for CAT Exam by using below quiz…
This paper has 50 questions.
Time allowed is 50 minutes.
The CAT Online Test Series 1st, CAT Free Online Test Exam is Very helpful for all students. Now Scroll down below n click on “Start Quiz” or “Start Test” and Test yourself.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 50 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Answered
- Review
-
Question 1 of 50
1. Question
A question paper consists of five problems, each problem having three internal choices. In how many ways can a candidate attempt one or more problems?
Correct
Given that, the question paper consists of five problems. For each problem, one or two or three or none of the choices can be attempted.
Hence, the required number of ways = 45 – 1.
= 210 – 1 = 1024 – 1 = 1023Incorrect
Given that, the question paper consists of five problems. For each problem, one or two or three or none of the choices can be attempted.
Hence, the required number of ways = 45 – 1.
= 210 – 1 = 1024 – 1 = 1023 -
Question 2 of 50
2. Question
The denominator of a fraction is 1 less than twice the numerator. If the numerator and denominator are both increased by 1, the fraction becomes 3/5. Find the fraction?
Correct
Let the numerator and denominator of the fraction be ‘n’ and ‘d’ respectively.
d = 2n – 1
(n + 1)/(d + 1) = 3/5
5n + 5 = 3d + 3
5n + 5 = 3(2n – 1) + 3 => n = 5
d = 2n – 1 => d = 9
Hence the fraction is : 5/9.Incorrect
Let the numerator and denominator of the fraction be ‘n’ and ‘d’ respectively.
d = 2n – 1
(n + 1)/(d + 1) = 3/5
5n + 5 = 3d + 3
5n + 5 = 3(2n – 1) + 3 => n = 5
d = 2n – 1 => d = 9
Hence the fraction is : 5/9. -
Question 3 of 50
3. Question
The number of arrangements that can be made with the letters of the word MEADOWS so that the vowels occupy the even places?
Correct
The word MEADOWS has 7 letters of which 3 are vowels.
-V-V-V-
As the vowels have to occupy even places, they can be arranged in the 3 even places in 3! i.e., 6 ways. While the consonants can be arranged among themselves in the remaining 4 places in 4! i.e., 24 ways.
Hence the total ways are 24 * 6 = 144.Incorrect
The word MEADOWS has 7 letters of which 3 are vowels.
-V-V-V-
As the vowels have to occupy even places, they can be arranged in the 3 even places in 3! i.e., 6 ways. While the consonants can be arranged among themselves in the remaining 4 places in 4! i.e., 24 ways.
Hence the total ways are 24 * 6 = 144. -
Question 4 of 50
4. Question
64 boys and 40 girls form a group for social work. During their membership drive, same number of boys and girls joined the group. How many members does the group have now, if the ratio of boys to girls is 4 : 3?
Correct
Let us say x boys and x girls joined the group.
(64 + x) / (40 + x) = 4/3
192 + 3x = 160 + 4x => x = 32
Number of members in the group = 64 + x + 40 + x
= 104 + 2x = 168.Incorrect
Let us say x boys and x girls joined the group.
(64 + x) / (40 + x) = 4/3
192 + 3x = 160 + 4x => x = 32
Number of members in the group = 64 + x + 40 + x
= 104 + 2x = 168. -
Question 5 of 50
5. Question
The length of a rectangular plot is thrice its breadth. If the area of the rectangular plot is 867 sq m, then what is the breadth of the rectangular plot?
Correct
Let the breadth of the plot be b m.
Length of the plot = 3 b m
(3b)(b) = 867
3b2 = 867
b2 = 289 = 172 (b > 0)
b = 17 m.Incorrect
Let the breadth of the plot be b m.
Length of the plot = 3 b m
(3b)(b) = 867
3b2 = 867
b2 = 289 = 172 (b > 0)
b = 17 m. -
Question 6 of 50
6. Question
Find the cost of fencing around a circular field of diameter 28 m at the rate of Rs.1.50 a meter?
Correct
2 * 22/7 * 14 = 88
88 * 1 1/2 = Rs.132Incorrect
2 * 22/7 * 14 = 88
88 * 1 1/2 = Rs.132 -
Question 7 of 50
7. Question
A and B can do a piece of work in 6 2/3 days and 5 days respectively. They work together for 2 days and then A leaves. In how many days after that B will complete the work alone.
Correct
3/20 * 2 + (2 + x)/5 = 1
x = 1 ½ daysIncorrect
3/20 * 2 + (2 + x)/5 = 1
x = 1 ½ days -
Question 8 of 50
8. Question
Find the one which does not belong to that group ?
Correct
Except in 862, in all other numbers sum of first two digits is same as the last digit.
Incorrect
Except in 862, in all other numbers sum of first two digits is same as the last digit.
-
Question 9 of 50
9. Question
Simplify the following:
(169/121)-3/2 * 27/2 * (13/22)-1Correct
(169/121)-3/2 * 27/2 * (13/22)-1
(132/112)-3/2 * 27/2 * 22/13 = 13-3/11-3 * 27/2 * 22/13
= 13-4 114 33Incorrect
(169/121)-3/2 * 27/2 * (13/22)-1
(132/112)-3/2 * 27/2 * 22/13 = 13-3/11-3 * 27/2 * 22/13
= 13-4 114 33 -
Question 10 of 50
10. Question
How much time will a train of length 200 m moving at a speed of 72 kmph take to cross another train of length 300 m, moving at 36 kmph in the same direction?
Correct
The distance to be covered = Sum of their lengths = 200 + 300 = 500 m.
Relative speed = 72 -36 = 36 kmph = 36 * 5/18 = 10 mps.
Time required = d/s = 500/10 = 50 sec.Incorrect
The distance to be covered = Sum of their lengths = 200 + 300 = 500 m.
Relative speed = 72 -36 = 36 kmph = 36 * 5/18 = 10 mps.
Time required = d/s = 500/10 = 50 sec. -
Question 11 of 50
11. Question
(562 – 242) * 1/32 + ?% of 1200 = 146
Correct
(562 – 242) * 1/32 + ?% of 1200 = 146
=> (3136 – 576) * 1/32 + ?/32 of 1200 = 146
=> 2560/32 + ? * 12 = 146 => ? * 12 = 146 – 80
=> ? = 66/12 => 5 1/2Incorrect
(562 – 242) * 1/32 + ?% of 1200 = 146
=> (3136 – 576) * 1/32 + ?/32 of 1200 = 146
=> 2560/32 + ? * 12 = 146 => ? * 12 = 146 – 80
=> ? = 66/12 => 5 1/2 -
Question 12 of 50
12. Question
The profit earned by selling an article for Rs. 832 is equal to the loss incurred when the same article is sold for Rs. 448. What should be the sale price for making 50% profit?
Correct
Let C.P. = Rs. x.
Then, 832 – x = x – 448
2x = 1280 => x = 640
Required S.P. = 150% of Rs. 640 = 150/100 * 640 = Rs. 960.Incorrect
Let C.P. = Rs. x.
Then, 832 – x = x – 448
2x = 1280 => x = 640
Required S.P. = 150% of Rs. 640 = 150/100 * 640 = Rs. 960. -
Question 13 of 50
13. Question
A train running at a speed of 36 kmph crosses an electric pole in 12 seconds. In how much time will it cross a 350 m long platform?
Correct
Let the length of the train be x m.
When a train crosses an electric pole, the distance covered is its own length.
So, x = 12 * 36 * 5 /18 m = 120 m.
Time taken to cross the platform = (120 +350)/ 36 * 5/18 = 47 min.Incorrect
Let the length of the train be x m.
When a train crosses an electric pole, the distance covered is its own length.
So, x = 12 * 36 * 5 /18 m = 120 m.
Time taken to cross the platform = (120 +350)/ 36 * 5/18 = 47 min. -
Question 14 of 50
14. Question
(3-3 * 95/2) / (272/3 * 3-4) = ?
Correct
(3-3 * 95/2) / (272/3 * 3-4) = [3-3 * (32)5/2] / [(33)2/3 * 3-4]
= (3-3 * 35) / (32 * 3-4) = (3-3+5)/(32-4) = 32/3-2 = 32 * 32 = 81.Incorrect
(3-3 * 95/2) / (272/3 * 3-4) = [3-3 * (32)5/2] / [(33)2/3 * 3-4]
= (3-3 * 35) / (32 * 3-4) = (3-3+5)/(32-4) = 32/3-2 = 32 * 32 = 81. -
Question 15 of 50
15. Question
The average runs scored by a batsman in 20 matches is 40. In the next 10 matches the batsman scored an average of 13 runs. Find his average in all the 30 matches?
Correct
Total score of the batsman in 20 matches = 800.
Total score of the batsman in the next 10 matches = 130.
Total score of the batsman in the 30 matches = 930.
Average score of the batsman = 930/30 = 31.Incorrect
Total score of the batsman in 20 matches = 800.
Total score of the batsman in the next 10 matches = 130.
Total score of the batsman in the 30 matches = 930.
Average score of the batsman = 930/30 = 31. -
Question 16 of 50
16. Question
If 3 workers collect 48 kg of cotton in 4 days, how many kg of cotton will 9 workers collect in 2 days?
Correct
(3 * 4)/48 = (9 * 2)/ x
x = 72 kgIncorrect
(3 * 4)/48 = (9 * 2)/ x
x = 72 kg -
Question 17 of 50
17. Question
In a 1000 m race, A beats B by 50 m and B beats C by 100 m. In the same race, by how many meters does A beat C?
Correct
By the time A covers 1000 m, B covers (1000 – 50) = 950 m.
By the time B covers 1000 m, C covers (1000 – 100) = 900 m.
So, the ratio of speeds of A and C =
1000/950 * 1000/900 = 1000/855 So, by the time A covers 1000 m, C covers 855 m.
So in 1000 m race A beats C by 1000 – 855 = 145 m.Incorrect
By the time A covers 1000 m, B covers (1000 – 50) = 950 m.
By the time B covers 1000 m, C covers (1000 – 100) = 900 m.
So, the ratio of speeds of A and C =
1000/950 * 1000/900 = 1000/855 So, by the time A covers 1000 m, C covers 855 m.
So in 1000 m race A beats C by 1000 – 855 = 145 m. -
Question 18 of 50
18. Question
A group of 10 representatives is to be selected out of 12 seniors and 10 juniors. In how many different ways can the group be selected if it should have at least one senior?
Correct
The total number of ways of forming the group of ten representatives is ²²C₁₀.
The total number of ways of forming the group that consists of no seniors is ¹⁰C₁₀ = 1 way
The required number of ways = ²²C₁₀ – 1Incorrect
The total number of ways of forming the group of ten representatives is ²²C₁₀.
The total number of ways of forming the group that consists of no seniors is ¹⁰C₁₀ = 1 way
The required number of ways = ²²C₁₀ – 1 -
Question 19 of 50
19. Question
I. a3 – 988 = 343,
II. b2 – 72 = 49 to solve both the equations to find the values of a and b?Correct
a3 = 1331 => a = 11
b2 = 121 => b = ± 11
a ≥ bIncorrect
a3 = 1331 => a = 11
b2 = 121 => b = ± 11
a ≥ b -
Question 20 of 50
20. Question
The slant height of a cone is 12 cm and radius of the base is 4cm, find the curved surface of the cone.
Correct
π * 12 * 4 = 48
Incorrect
π * 12 * 4 = 48
-
Question 21 of 50
21. Question
A wire in the form of a circle of radius 3.5 m is bent in the form of a rectangule, whose length and breadth are in the ratio of 6 : 5. What is the area of the rectangle?
Correct
The circumference of the circle is equal to the permeter of the rectangle.
Let l = 6x and b = 5x 2(6x + 5x) = 2 * 22/7 * 3.5
=> x = 1
Therefore l = 6 cm and b = 5 cm Area of the rectangle = 6 * 5 = 30 cm2Incorrect
The circumference of the circle is equal to the permeter of the rectangle.
Let l = 6x and b = 5x 2(6x + 5x) = 2 * 22/7 * 3.5
=> x = 1
Therefore l = 6 cm and b = 5 cm Area of the rectangle = 6 * 5 = 30 cm2 -
Question 22 of 50
22. Question
Find the one which does not belong to that group ?
Correct
Skin, Eye, Nose and Ear are sensory organs, while Leg is a limb.
Incorrect
Skin, Eye, Nose and Ear are sensory organs, while Leg is a limb.
-
Question 23 of 50
23. Question
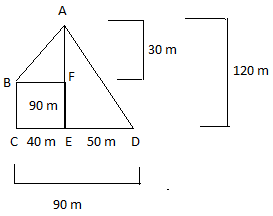
A plot ABCD is as shown in figure, where AF = 30 m, CE = 40 m, ED = 50 m, AE = 120 m. Find the area of the plot ABCD?Correct
Area of plot ABCD = Area of ADE + Area of AFB + Area of BCEF = 1/2 * 50 * 120 + 1/2 * 40 * 30 + 40 * 90 = 3000 + 600 + 3600 = 7200 sq.m
Incorrect
Area of plot ABCD = Area of ADE + Area of AFB + Area of BCEF = 1/2 * 50 * 120 + 1/2 * 40 * 30 + 40 * 90 = 3000 + 600 + 3600 = 7200 sq.m
-
Question 24 of 50
24. Question
The average of first 10 prime numbers is?
Correct
Sum of 10 prime no. = 129
Average = 129/10 = 12.9Incorrect
Sum of 10 prime no. = 129
Average = 129/10 = 12.9 -
Question 25 of 50
25. Question
? % of 400 + 40% of 160 = 17% of 400
Correct
? % of 400 + 40% of 160 = 17% of 400
?/100 of 400 + 40/100 of 160 = 17/100 of 400
?(4) + 64 = 68 => ? = 1Incorrect
? % of 400 + 40% of 160 = 17% of 400
?/100 of 400 + 40/100 of 160 = 17/100 of 400
?(4) + 64 = 68 => ? = 1 -
Question 26 of 50
26. Question
A laborer is engaged for 30 days on the condition that he receives Rs.25 for each day he works and is fined Rs.7.50 for each day is absent. He gets Rs.425 in all. For how many days was he absent?
Correct
30 * 25 = 750
425
———–
325
25 + 7.50 = 32.5
325/32.5 = 10Incorrect
30 * 25 = 750
425
———–
325
25 + 7.50 = 32.5
325/32.5 = 10 -
Question 27 of 50
27. Question
A and B starts a business with Rs.8000 each, and after 4 months, B withdraws half of his capital . How should they share the profits at the end of the 18 months?
Correct
A invests Rs.8000 for 18 months, but B invests Rs.8000 for the first 4 months and then withdraws Rs.4000. So, the investment of B for remaining 14 months is Rs.4000 only.
A : B
8000*18 : (8000*4) + (4000*14)
14400 : 88000
A:B = 18:11Incorrect
A invests Rs.8000 for 18 months, but B invests Rs.8000 for the first 4 months and then withdraws Rs.4000. So, the investment of B for remaining 14 months is Rs.4000 only.
A : B
8000*18 : (8000*4) + (4000*14)
14400 : 88000
A:B = 18:11 -
Question 28 of 50
28. Question
If the sum of one-half of a number exceeds one-third of that number by 7 1/3, the number is:
Correct
Let the number be x. Then,
(1/2 x + 1/5 x) – 1/3 x = 22/3
11/30 x = 22/3
x = 20Incorrect
Let the number be x. Then,
(1/2 x + 1/5 x) – 1/3 x = 22/3
11/30 x = 22/3
x = 20 -
Question 29 of 50
29. Question
What is the difference between the largest number and the least number written with the digits 7, 3, 1, 4?
Correct
1347
7431
————
6084Incorrect
1347
7431
————
6084 -
Question 30 of 50
30. Question
The area of the square formed on the diagonal of a rectangle as its side is 108 1/3 % more than the area of the rectangle. If the perimeter of the rectangle is 28 units, find the difference between the sides of the rectangle?
Correct
Let the sides of the rectangle be l and b respectively.
From the given data,
(√l2 + b2) = (1 + 108 1/3 %)lb
=> l2 + b2 = (1 + 325/3 * 1/100)lb
= (1 + 13/12)lb
= 25/12 lb
=> (l2 + b2)/lb = 25/12
12(l2 + b2) = 25lb
Adding 24lb on both sides
12l2 + 12b2 + 24lb = 49lb
12(l2 + b2 + 2lb) = 49lb
but 2(l + b) = 28 => l + b = 14
12(l + b)2 = 49lb
=> 12(14)2 = 49lb
=> lb = 48
Since l + b = 14, l = 8 and b = 6
l – b = 8 – 6 = 2m.Incorrect
Let the sides of the rectangle be l and b respectively.
From the given data,
(√l2 + b2) = (1 + 108 1/3 %)lb
=> l2 + b2 = (1 + 325/3 * 1/100)lb
= (1 + 13/12)lb
= 25/12 lb
=> (l2 + b2)/lb = 25/12
12(l2 + b2) = 25lb
Adding 24lb on both sides
12l2 + 12b2 + 24lb = 49lb
12(l2 + b2 + 2lb) = 49lb
but 2(l + b) = 28 => l + b = 14
12(l + b)2 = 49lb
=> 12(14)2 = 49lb
=> lb = 48
Since l + b = 14, l = 8 and b = 6
l – b = 8 – 6 = 2m. -
Question 31 of 50
31. Question
The inverse ratio of 3: 2: 1 is?
Correct
1/3: 1/2: 1/1 = 2:3:6
Incorrect
1/3: 1/2: 1/1 = 2:3:6
-
Question 32 of 50
32. Question
The wheels revolve round a common horizontal axis. They make 15, 20 and 48 revolutions in a minute respectively. Starting with a certain point on the circumference down wards. After what interval of time will they come together in the same position?
Correct
Time for one revolution = 60/15 = 4
60/ 20 = 3
60/48 = 5/4
LCM of 4, 3, 5/4
LCM of Numerators/HCF of Denominators =
60/1 = 60Incorrect
Time for one revolution = 60/15 = 4
60/ 20 = 3
60/48 = 5/4
LCM of 4, 3, 5/4
LCM of Numerators/HCF of Denominators =
60/1 = 60 -
Question 33 of 50
33. Question
If x % of 80 = 20% of y, then x = ? and y = ?
Correct
x % of 80 = 20 % of y => x / 100 (80) = 20 / 100 (y)
=> 4x = y
i.e x / y = ¼Incorrect
x % of 80 = 20 % of y => x / 100 (80) = 20 / 100 (y)
=> 4x = y
i.e x / y = ¼ -
Question 34 of 50
34. Question
The distance between Delhi and Mathura is 110 kms. A starts from Delhi with a speed of 20 kmph at 7 a.m. for Mathura and B starts from Mathura with a speed of 25 kmph at 8 p.m. from Delhi. When will they meet?
Correct
D = 110 – 20 = 90
RS = 20 + 25 = 45
T = 90/45 = 2 hours
8 a.m. + 2 = 10 a.m.Incorrect
D = 110 – 20 = 90
RS = 20 + 25 = 45
T = 90/45 = 2 hours
8 a.m. + 2 = 10 a.m. -
Question 35 of 50
35. Question
A train 125 m long passes a man, running at 5 km/hr in the same direction in which the train is going, in 10 sec. The speed of the train is?
Correct
Speed of the train relative to man = 125/10 = 25/2 m/sec.
= 25/2 * 18/5 = 45 km/hr
Let the speed of the train be x km/hr. Then, relative speed = (x – 5) km/hr.
x – 5 = 45 => x = 50 km/hr.Incorrect
Speed of the train relative to man = 125/10 = 25/2 m/sec.
= 25/2 * 18/5 = 45 km/hr
Let the speed of the train be x km/hr. Then, relative speed = (x – 5) km/hr.
x – 5 = 45 => x = 50 km/hr. -
Question 36 of 50
36. Question
The average weight of a group of persons increased from 48 kg to 51 kg, when two persons weighing 78 kg and 93 kg join the group. Find the initial number of members in the group?
Correct
Let the initial number of members in the group be n.
Initial total weight of all the members in the group = n(48)
From the data,
48n + 78 + 93 = 51(n + 2) => 51n – 48n = 69 => n = 23
Therefore there were 23 members in the group initially.Incorrect
Let the initial number of members in the group be n.
Initial total weight of all the members in the group = n(48)
From the data,
48n + 78 + 93 = 51(n + 2) => 51n – 48n = 69 => n = 23
Therefore there were 23 members in the group initially. -
Question 37 of 50
37. Question
Two trains each 250 m in length are running on the same parallel lines in opposite directions with the speed of 80 kmph and 70 kmph respectively. In what time will they cross each other completely?
Correct
D = 250 m + 250 m = 500 m
RS = 80 + 70 = 150 * 5/18 = 125/3
T = 500 * 3/125 = 12 secIncorrect
D = 250 m + 250 m = 500 m
RS = 80 + 70 = 150 * 5/18 = 125/3
T = 500 * 3/125 = 12 sec -
Question 38 of 50
38. Question
If a person walks at 14 km/hr instead of 10 km/hr, he would have walked 20 km more. The actual distance traveled by him is?
Correct
Let the actual distance traveled be x km. Then,
x/10 = (x + 20)/14
4x – 200 =>x = 50 km.Incorrect
Let the actual distance traveled be x km. Then,
x/10 = (x + 20)/14
4x – 200 =>x = 50 km. -
Question 39 of 50
39. Question
The weights of three boys are in the ratio 4 : 5 : 6. If the sum of the weights of the heaviest and the lightest boy is 45 kg more than the weight of the third boy, what is the weight of the lightest boy?
Correct
Let the weights of the three boys be 4k, 5k and 6k respectively.
4k + 6k = 5k + 45
=> 5k = 45 => k = 9
Therefore the weight of the lightest boy
= 4k = 4(9) = 36 kg.Incorrect
Let the weights of the three boys be 4k, 5k and 6k respectively.
4k + 6k = 5k + 45
=> 5k = 45 => k = 9
Therefore the weight of the lightest boy
= 4k = 4(9) = 36 kg. -
Question 40 of 50
40. Question
The speed of a train is 90 kmph. What is the distance covered by it in 10 minutes?
Correct
90 * 10/60 = 15 kmph
Incorrect
90 * 10/60 = 15 kmph
-
Question 41 of 50
41. Question
If p, q and r are positive integers and satisfy x = (p + q -r)/r = (p – q + r)/q = (q + r – p)/p, then the value of x is?
Correct
When two or more ratios are equal, each of the ratios are equal to sum of the numerators divided by the sum of the denominators, provided sum of the denominators is non-zero.
Hence, x = (p + q -r)/r = (p – q + r)/q = (q + r – p)/p
=> x = (p + q – r + p – q + r + q + r – p) / (r + q + p)
=> x = (r + q + p) / (r + q + p) = 1
p + q + r is non-zero.Incorrect
When two or more ratios are equal, each of the ratios are equal to sum of the numerators divided by the sum of the denominators, provided sum of the denominators is non-zero.
Hence, x = (p + q -r)/r = (p – q + r)/q = (q + r – p)/p
=> x = (p + q – r + p – q + r + q + r – p) / (r + q + p)
=> x = (r + q + p) / (r + q + p) = 1
p + q + r is non-zero. -
Question 42 of 50
42. Question
Find the one which does not belong to that group ?
Correct
Crocodile, Turtle, Allegator and Frog are amphibians, while Chameleon is a terrestrial animal.
Incorrect
Crocodile, Turtle, Allegator and Frog are amphibians, while Chameleon is a terrestrial animal.
-
Question 43 of 50
43. Question
A train 150 m long running at 72 kmph crosses a platform in 25 sec. What is the length of the platform?
Correct
D = 72 * 5/18 = 25 = 500 – 150 = 350
Incorrect
D = 72 * 5/18 = 25 = 500 – 150 = 350
-
Question 44 of 50
44. Question
64 is what percent of 80?
Correct
Let x percent of 80 be 64.
80 * x/100 = 64 => x = (64 * 100)/80 => x = 80.
80% of 80 is 64.Incorrect
Let x percent of 80 be 64.
80 * x/100 = 64 => x = (64 * 100)/80 => x = 80.
80% of 80 is 64. -
Question 45 of 50
45. Question
A brick measures 20 cm * 10 cm * 7.5 cm how many bricks will be required for a wall 25 m * 2 m * 0.75 m?
Correct
25 * 2 * 0.75 = 20/100 * 10/100 * 7.5/100 * x
25 = 1/100 * x => x = 25000Incorrect
25 * 2 * 0.75 = 20/100 * 10/100 * 7.5/100 * x
25 = 1/100 * x => x = 25000 -
Question 46 of 50
46. Question
The sum of five consecutive odd numbers of set p is 435. What is the sum of five consecutive numbers of another set q. Whose largest number is 45 more than the largest number of set p?
Correct
Let the five consecutive odd numbers of set p be 2n – 3, 2n – 1, 2n + 1, 2n + 3, 2n + 5.
Sum of these five numbers
= 2n – 3 + 2n – 1 + 2n + 1 + 2n + 3 + 2n + 5
= 10n + 5 = 435 => n = 43
Largest number of set p = 2(43) + 5 = 91
The largest number of set q = 91 + 45 = 136
=> The five numbers of set q are 132, 133, 134, 135, 136.
Sum of above numbers = 132 + 133 + 134 + 135 + 136 = 670.Incorrect
Let the five consecutive odd numbers of set p be 2n – 3, 2n – 1, 2n + 1, 2n + 3, 2n + 5.
Sum of these five numbers
= 2n – 3 + 2n – 1 + 2n + 1 + 2n + 3 + 2n + 5
= 10n + 5 = 435 => n = 43
Largest number of set p = 2(43) + 5 = 91
The largest number of set q = 91 + 45 = 136
=> The five numbers of set q are 132, 133, 134, 135, 136.
Sum of above numbers = 132 + 133 + 134 + 135 + 136 = 670. -
Question 47 of 50
47. Question
36 * 48 ÷ 64 + 36 ÷ 12 = ?
Correct
36 * 48 / 64 + 36/12 = 27 + 3 = 30
Incorrect
36 * 48 / 64 + 36/12 = 27 + 3 = 30
-
Question 48 of 50
48. Question
The average age of three boys is 15 years and their ages are in proportion 3:5:7. What is the age in years of the youngest boy?
Correct
3x + 5x + 7x = 45
x =3
3x = 9Incorrect
3x + 5x + 7x = 45
x =3
3x = 9 -
Question 49 of 50
49. Question
Sides of a rectangular park are in the ratio 3: 2 and its area is 3750 sq m, the cost of fencing it at 50 ps per meter is?
Correct
3x * 2x = 3750 => x = 25
2(75 + 50) = 250 m
250 * 1/2 = Rs.125Incorrect
3x * 2x = 3750 => x = 25
2(75 + 50) = 250 m
250 * 1/2 = Rs.125 -
Question 50 of 50
50. Question
If A got 80 marks and B got 60 marks, then what percent of A’s mark is B’s mark?
Correct
A’s marks = 80 ; B’s marks = 60.
Let x% of A = B => x/100 * 80 = 60
=> x = (60 * 100)/80 = 75
B’s marks is 75% of A’s marks.Incorrect
A’s marks = 80 ; B’s marks = 60.
Let x% of A = B => x/100 * 80 = 60
=> x = (60 * 100)/80 = 75
B’s marks is 75% of A’s marks.