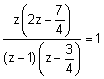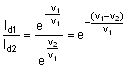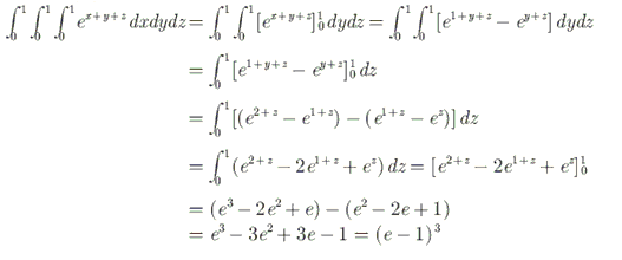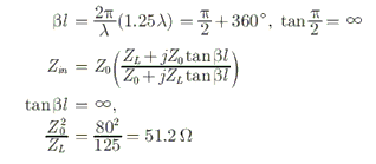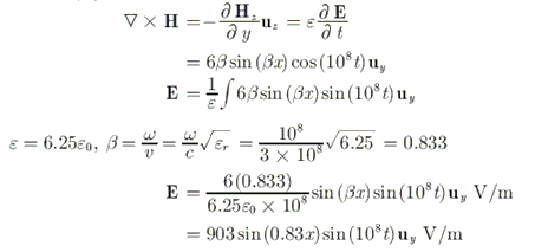GATE Electronics and Communication Online Test Series 1
Finish Quiz
0 of 25 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
Information
GATE Electronics and Communication Online Test Series 1. GATE 2021 EC Online Test, GATE Mock Test Exam 2021.GATE Electronics and Communication Full online mock test paper is free for all students. Take GATE 2021 Exams Online Test, GATE 2021 Quiz. GATE 2021 EC Series 1 online Test 2021 in English. Take GATE 2021 Mock Test in English from below, GATE Quiz 2021 Series 1. You may also find other Subjects GATE Online Test in this page. Here we provide Graduate Aptitude Test in Engineering Question and Answers 2021. This GATE EC Online test Series 1 is very helpful for exam preparation. The GATE Electronics and Communication Mock Test 2021 is now available for all candidates, who will be appearing in the national level engineering exams 2021. Now take GATE Electronics and Communication Online Test Series 1 by Click on Below “Start Quiz Button”
This paper has 25 questions.
Time allowed is 30 minutes.
GATE Electronics and Communication online Mock Test Exam is Very helpful for all students. Now Scroll down below n click on “Start Quiz” or “Start Test” and Test yourself.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 25 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- Answered
- Review
-
Question 1 of 25
1. Question
is equal to
Correct
Incorrect
-
Question 2 of 25
2. Question
Consider a ufb system with forward-path transfer function G (s) =
. The system is stable for the range of K. Which of the following is correct?
Correct
G(s) = k(s+3)/s^4(s+2)
We can write as
G(s) = k(s+3)/(s^5+2s^4+ks+1)
The system is always unstable because s3 and s2 are missing here.Incorrect
G(s) = k(s+3)/s^4(s+2)
We can write as
G(s) = k(s+3)/(s^5+2s^4+ks+1)
The system is always unstable because s3 and s2 are missing here. -
Question 3 of 25
3. Question
The time signal corresponding to
is
Correct
Option (1) is correct.
X (s) = 2 – 1 / (s+2) (s+3)
= 2 – 1 / (s+2) + 1 / (s+3)
X (t) = 2(t) + (e-3t – e-2t) u (t)Incorrect
Option (1) is correct.
X (s) = 2 – 1 / (s+2) (s+3)
= 2 – 1 / (s+2) + 1 / (s+3)
X (t) = 2(t) + (e-3t – e-2t) u (t) -
Question 4 of 25
4. Question
The characteristic equation of a closed-loop system is s(s + 1)(s + 2) + k = 0. The centroid of the asymptotes in root-locus will be
Correct
Option (2) is correct.
Sum of poles = 0-1-2 = -3
Sum of zeros = 0
Therefore, no. of poles – no.of zeros = N. of values for which response is infinite = 3 poles and none zeros. Hence,Incorrect
Option (2) is correct.
Sum of poles = 0-1-2 = -3
Sum of zeros = 0
Therefore, no. of poles – no.of zeros = N. of values for which response is infinite = 3 poles and none zeros. Hence, -
Question 5 of 25
5. Question
Given the z – transform X (z) =
, the limit of x [∞] is
Correct
Option (1) is correct.
The function has poles at z = 1, 3/4 . Thus, the final value theorem applies.
= (z – 1)
Incorrect
Option (1) is correct.
The function has poles at z = 1, 3/4 . Thus, the final value theorem applies.
= (z – 1)
-
Question 6 of 25
6. Question
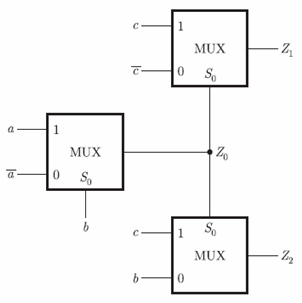
A MUX network is shown below.
The function Z1 is equal to 1 whenCorrect
According to the circuit of MUXs: Z1 = 1 when Z0 = 0 otherwise Z1 is equal to 0. Z0 = 0 when b = 1, at this time a = 0. So, Z1 = a’ . b. c .
This is the correct answer. Also one cannot represent the operation of MUX in simple binary expression unless the conditions are met.Incorrect
According to the circuit of MUXs: Z1 = 1 when Z0 = 0 otherwise Z1 is equal to 0. Z0 = 0 when b = 1, at this time a = 0. So, Z1 = a’ . b. c .
This is the correct answer. Also one cannot represent the operation of MUX in simple binary expression unless the conditions are met. -
Question 7 of 25
7. Question
If (211)x = (152)8, the value of base x is
Correct
Option (3) is correct.
2x2 + x + 1 = 64 + 5 x 8 + 2
x = 7Incorrect
Option (3) is correct.
2x2 + x + 1 = 64 + 5 x 8 + 2
x = 7 -
Question 8 of 25
8. Question
An ideal pn junction diode is operating in the forward bias region. The change in diode voltage, that will cause a factor of 9 increase in current, is
Correct
Id = Is
V1 – V2 = Vt In= 0.0259 In 10 = 59.6 mV ≈ 59mV
Incorrect
Id = Is
V1 – V2 = Vt In= 0.0259 In 10 = 59.6 mV ≈ 59mV
-
Question 9 of 25
9. Question
If the base width of a bi-polar transistor is increased by a factor of 3, what is the collector current change?
Correct
We know
Ic =
IC
So, if WB increases by a factor of 3, then IC is decreased by a factor of 3.Incorrect
We know
Ic =
IC
So, if WB increases by a factor of 3, then IC is decreased by a factor of 3. -
Question 10 of 25
10. Question
For a n-channel enhancement-mode MOSFET, the parameters are VTN = 0.8 V, k’n = 80 mA/V2 and W/L = 5. If the transistor is biased in saturation region with ID = 0.5 mA, then required VGB is
Correct
0.5 =
VGS =+ 0.8 = 2.38 V
Incorrect
0.5 =
VGS =+ 0.8 = 2.38 V
-
Question 11 of 25
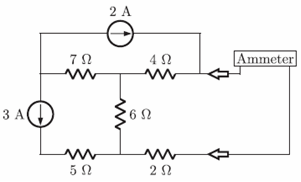
11. Question
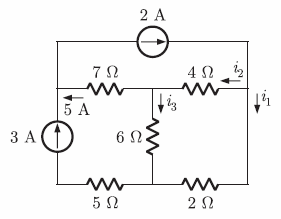
The value of the current measured by the ammeter in figure is
Correct
4i2 + 6i3 – 2i1 = 0
i1 + i2 = 2
i2 = 5 + i3
i1 = -5/6 A
Incorrect
4i2 + 6i3 – 2i1 = 0
i1 + i2 = 2
i2 = 5 + i3
i1 = -5/6 A
-
Question 12 of 25
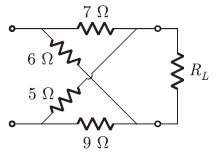
12. Question
In the following lattice network, the value of RL for the maximum power transfer to it is
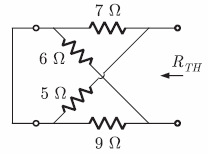
Correct
The circuit is as shown below.
TTH = 7 || 5 + 6 || 9 = 6.52 Ω
For maximum power transfer
RL = TTH = 6.52 ΩIncorrect
The circuit is as shown below.
TTH = 7 || 5 + 6 || 9 = 6.52 Ω
For maximum power transfer
RL = TTH = 6.52 Ω -
Question 13 of 25
13. Question
Let J =
uz A/m2. The value of
is
Correct
== 0
Incorrect
== 0
-
Question 14 of 25
14. Question
A vector field is given by E = 4zy2ux + 2y sin 2xuy + y2 sin 2xuz. The surface on which Ey = 0 is
Correct
For Ey = 0, 2y sin 2x = 0
y = 0
sin 2x = 0
2x = 0, π,3π
x = 0, 3π/2Incorrect
For Ey = 0, 2y sin 2x = 0
y = 0
sin 2x = 0
2x = 0, π,3π
x = 0, 3π/2 -
Question 15 of 25
15. Question
In a nonmagnetic medium, E = 5 cos (109 t – 8x) ux + 4 sin (109 t – 8x) uz V/m. The dielectric constant of the medium is
Correct
Incorrect
-
Question 16 of 25
16. Question
The aerial current of an AM transmitter is 18 A when unmodulated but increases to 20 A when modulated.
The modulation index isCorrect
It = Ic
= 0.68
Incorrect
It = Ic
= 0.68
-
Question 17 of 25
17. Question
A carrier is phase modulated (PM) with frequency deviation of 10 kHz by a signal tone frequency of 1 kHz. If the signal tone frequency is increased to 2 kHz, assuming that phase deviation remains unchanged, the bandwidth of the PM signal is
Correct
Initial 4 x 10 = 40 kHz
Now if deviation is d, then Δ BW = 2d = 2 x 2 = 4 kHz
New Bandwidth BW = 40 + 4 = 44 kHzIncorrect
Initial 4 x 10 = 40 kHz
Now if deviation is d, then Δ BW = 2d = 2 x 2 = 4 kHz
New Bandwidth BW = 40 + 4 = 44 kHz -
Question 18 of 25
18. Question
A dice is thrown thrice. Getting 1 or 6 is taken as a success. The mean of the number of successes is
Correct
p =
, q =
and n = 3
Thus, mean (np) = 1/3×3 = 1Incorrect
p =
, q =
and n = 3
Thus, mean (np) = 1/3×3 = 1 -
Question 19 of 25
19. Question
Let f (x) = ex in [0, 1], the value of c of the mean – value theorem is
Correct
f` (c) =
c = log (e – 1)Incorrect
f` (c) =
c = log (e – 1) -
Question 20 of 25
20. Question
For dy/dx = xy, we have y = 1 at x = 0. By using Euler method and taking the step size 0.1, find the value of y at x = 0.4.
Correct
x : 0 0.1 0.2 0.3 0.4
Euler method gives:
yn+1 = yn + h (xn, yn) …………. (1)
n = 0 in (1) gives:
y1 = |y0 + h f (x0, y0)|
Here x0 = 0,
y0 = 1,
h = 0.1
y1 = 1 + 0.1 f (0, 1) = 1 + 0 = 1
n = 0 in (1) gives y2 = y1 + hf (x1, y1)
= 1 + 0.1 f (0.1, 1) = 1 + 0.1 (0.1) = 1 + 0.01
Thus y2 = y(0, 2) = 1.01
n = 2 in (1) gives:
y3 = y2 + hf (|x2, y2) = 1.01 + 0.1 f (0.2, 1.01)
y3 = y(0, 3) = 1.01 + 0.0202 = 1.0302
n = 2 in (1) gives:
y3 = y2 + hf (x2, y2) = 1.01 + 0.1 f (0.2, 1.01)
y3 = y(0, 3) = 1.01 + 0.0202 = 1.0302
n = 3 in (1) gives:
y4 = y3 + hf (x3, y3) = 1.0302 + 0.1 f (0.3, 1.0302)
= 1.0302 + 0.03090
Hence y4 = y(0, 4) = 1.0611Incorrect
x : 0 0.1 0.2 0.3 0.4
Euler method gives:
yn+1 = yn + h (xn, yn) …………. (1)
n = 0 in (1) gives:
y1 = |y0 + h f (x0, y0)|
Here x0 = 0,
y0 = 1,
h = 0.1
y1 = 1 + 0.1 f (0, 1) = 1 + 0 = 1
n = 0 in (1) gives y2 = y1 + hf (x1, y1)
= 1 + 0.1 f (0.1, 1) = 1 + 0.1 (0.1) = 1 + 0.01
Thus y2 = y(0, 2) = 1.01
n = 2 in (1) gives:
y3 = y2 + hf (|x2, y2) = 1.01 + 0.1 f (0.2, 1.01)
y3 = y(0, 3) = 1.01 + 0.0202 = 1.0302
n = 2 in (1) gives:
y3 = y2 + hf (x2, y2) = 1.01 + 0.1 f (0.2, 1.01)
y3 = y(0, 3) = 1.01 + 0.0202 = 1.0302
n = 3 in (1) gives:
y4 = y3 + hf (x3, y3) = 1.0302 + 0.1 f (0.3, 1.0302)
= 1.0302 + 0.03090
Hence y4 = y(0, 4) = 1.0611 -
Question 21 of 25
21. Question
The solution of dy/dx -y tan x – y2 sec x = 0 is given by
Correct
dy/dx – y tan x = y2 sec x
Or y-2 dy/dx – y-1 tan x = sec x
Put y-1 = v to get – y2 dy/dx = dv/dx
Substituting this in the given equation, we get
-dv/dx -v tan x = sec x or dv/dx + (tan x). v = – sec x
I. F =
v. sec x = –+ c = – tan x + c
1/y = = – sin x + cos x
Or y-1 = – sin x + c2 cos xIncorrect
dy/dx – y tan x = y2 sec x
Or y-2 dy/dx – y-1 tan x = sec x
Put y-1 = v to get – y2 dy/dx = dv/dx
Substituting this in the given equation, we get
-dv/dx -v tan x = sec x or dv/dx + (tan x). v = – sec x
I. F =
v. sec x = –+ c = – tan x + c
1/y = = – sin x + cos x
Or y-1 = – sin x + c2 cos x -
Question 22 of 25
22. Question
dxdydz is equal to
Correct
Incorrect
-
Question 23 of 25
23. Question
A lossless transmission line with a characteristic impedance of 80 Ω is terminated by a load of 125 Ω . The length of line is 1.25
. The input impedance is
Correct
Incorrect
-
Question 24 of 25
24. Question
In a non-magnetic medium (εr = 6.25), the magnetic field of an EM wave is
H = 6 cos β x cos (108 t) us A/m. The corresponding electric field isCorrect
Incorrect
-
Question 25 of 25
25. Question
The plane 2x + 3y – 4z = 1 separates two regions. Let µr1 = 2 in region 1 defined by 2x + 3y – 4z > 1, while µr1 = 5 in region 2 where 2x + 3y – 4z < 1. The region H1 = 50 ux – 30 uy + 20 uz A/m. In region 2, H2 will be
Correct
From the given solution Ht2 = 54.8Ux – 22.76 Uy + 10.34 Uz Hn2 = -1.93 Ux – 2.9Uy + 3.86 Uz H2 = Ht2 + Hn2 H2 = 52.87Ux -25.66 Uy + 14.2 Uz
Incorrect
From the given solution Ht2 = 54.8Ux – 22.76 Uy + 10.34 Uz Hn2 = -1.93 Ux – 2.9Uy + 3.86 Uz H2 = Ht2 + Hn2 H2 = 52.87Ux -25.66 Uy + 14.2 Uz