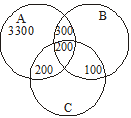JEE Main Mathematics Sets and Relations Online Test
Finish Quiz
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
JEE Main Mathematics Sets and Relations Online Test. JEE Main Online Test for Mathematics Sets and Relations. JEE Main Full Online Quiz for Mathematics Sets and Relations. JEE Main Free Mock Test Paper 2021. JEE Main 2021 Free Online Practice Test, Take JEE Online Test for All Subjects. JEE Main Question and Answers for Mathematics Sets and Relations. In this test You may find JEE Main all subjects Questions with Answers. Check JEE Main Question and Answers in English. This mock Test is free for All Students. Mock Test Papers are very helpful for Exam Purpose, by using below Mock Test Paper you may Test your Study for Next Upcoming Exams. Now Scroll down below n Take JEE Main Mathematics Sets and Relations…
This paper has 20 questions.
Time allowed is 30 minutes.
The JEE Main Mathematics Sets and Relations is Very helpful for all students. Now Scroll down below n click on “Start Quiz” or “Start Test” and Test yourself.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
-
Question 1 of 20
1. Question
Let n(a) = m and b = (n). Then, the total number of non-empty relations that can be defined from A to B is
Correct
Given , n(A) = m and n(B) = n
∴ Total number of relations from A to B = 2mn
∴ Total number of non-empty relations from A to B = 2mn –1
Incorrect
Given , n(A) = m and n(B) = n
∴ Total number of relations from A to B = 2mn
∴ Total number of non-empty relations from A to B = 2mn –1
-
Question 2 of 20
2. Question
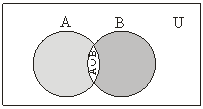
If A and B are two sets then (A – B) ∪ (B – A) ∪ (A ∩ B) is equal to
Correct
From Venn-Euler’s diagram,
∴ (A – B) ∪ (B – A) ∪ (A ∩ B) = A ∪ B.
Incorrect
From Venn-Euler’s diagram,
∴ (A – B) ∪ (B – A) ∪ (A ∩ B) = A ∪ B.
-
Question 3 of 20
3. Question
R is a relation from (11, 12, 13) to (8, 10, 12) defined by y = x – 3 The relation R-1 is
Correct
Let A = {11, 12, 13}, B = {8, 10, 12}
∴ R = {(11, 8), (13, 10)}
R-1 = {(8, 11), (10, 13)}
Incorrect
Let A = {11, 12, 13}, B = {8, 10, 12}
∴ R = {(11, 8), (13, 10)}
R-1 = {(8, 11), (10, 13)}
-
Question 4 of 20
4. Question
Let A = {1, 2, 3}. The total number of distinct relations that can be defined over A is
Correct
n(A × A) = n(A). n(A) = 32 = 9
So, the total number of subsets of A × A is 29 and a subset of A × A is a relation over the set A.
Incorrect
n(A × A) = n(A). n(A) = 32 = 9
So, the total number of subsets of A × A is 29 and a subset of A × A is a relation over the set A.
-
Question 5 of 20
5. Question
Let a relation R be defined by R = {(4, 5), (1, 4), (4, 6), (7, 6), (3, 7)}. The relation R-1 or is given by
Correct
Given, R = {(4, 5), (1, 4), (4, 6), (7, 6), (3, 7)}
∴ R-1 = {(5, 4), (4, 1), (6, 4), (6, 7), (7, 3)}
⇒ R-1 or = {(4, 4), (1, 1), (4, 7), (7, 4), (7, 7), (3, 3)}
Incorrect
Given, R = {(4, 5), (1, 4), (4, 6), (7, 6), (3, 7)}
∴ R-1 = {(5, 4), (4, 1), (6, 4), (6, 7), (7, 3)}
⇒ R-1 or = {(4, 4), (1, 1), (4, 7), (7, 4), (7, 7), (3, 3)}
-
Question 6 of 20
6. Question
The solution set of the equation x3 – 3x + 2 = 0 in roster from is
Correct
On solving x3 – 3x + 2 = 0
we get x = 1 & -2
∴ Solution set is {1, -2}
Incorrect
On solving x3 – 3x + 2 = 0
we get x = 1 & -2
∴ Solution set is {1, -2}
-
Question 7 of 20
7. Question
The relation R defined on the set of natural numbers as {(a, b) : a differs from b by 3}, is given by
Correct
Given, R = {(a, b) : a – b = 3} = {(4, 1) (5, 2), (6, 3), …………….}
Incorrect
Given, R = {(a, b) : a – b = 3} = {(4, 1) (5, 2), (6, 3), …………….}
-
Question 8 of 20
8. Question
Let A = {1, 2, 3, 4} and R be a relation in A given by R =
{(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (2, 1), (3, 1), (1, 3)}. Then R is
Correct
(1, 1), (2, 2), (3, 3), (4, 4) ∈ R; ∴ R is reflexive.
∵ (1, 2), (3, 1) ∈ R and also (2, 1), (1, 3) ∈ R.
Hence, R is synmetric. But clearly R is not transitive.
Incorrect
(1, 1), (2, 2), (3, 3), (4, 4) ∈ R; ∴ R is reflexive.
∵ (1, 2), (3, 1) ∈ R and also (2, 1), (1, 3) ∈ R.
Hence, R is synmetric. But clearly R is not transitive.
-
Question 9 of 20
9. Question
Let R be the relation from A = {2, 3, 4, 5} to B = {3, 6, 7, 10} defined by ‘x devides y’, then R-1 is equal to
Correct
Given, A = {2, 3, 4, 5} and B = {3, 6, 7, 10}
∴ R = {(2, 6), (2, 10), (3, 3), (3, 6), (5, 10)}
⇒ R-1 = {(6, 2), (10, 2), (3, 3), (6, 3), (10, 5)}
Incorrect
Given, A = {2, 3, 4, 5} and B = {3, 6, 7, 10}
∴ R = {(2, 6), (2, 10), (3, 3), (3, 6), (5, 10)}
⇒ R-1 = {(6, 2), (10, 2), (3, 3), (6, 3), (10, 5)}
-
Question 10 of 20
10. Question
If R is an equivalence relation on a set A, then R–1 is NOT
Correct
Incorrect
-
Question 11 of 20
11. Question
If R is a relation from a set A to the set B and S is a relation from B to C, then the relation SoR
Correct
Give, R ⊆ A × B and S ⊆ B × B, we have
So r ⊆ A × C
∴ SoR is a relation from A to C.
Incorrect
Give, R ⊆ A × B and S ⊆ B × B, we have
So r ⊆ A × C
∴ SoR is a relation from A to C.
-
Question 12 of 20
12. Question
The number of elements in the power set of {a, b, c}
Correct
Number of subsets of {a, b, c} = 23 = 8 ∴ number of elements in the power set = 8
Incorrect
Number of subsets of {a, b, c} = 23 = 8 ∴ number of elements in the power set = 8
-
Question 13 of 20
13. Question
The set {0, 2, 6, 12, 20} in the set-builder form is
Correct
We see that each number in the given set follow the relation x = n2 – 3n + 2 as for
n = 1, x = 1 – 3 + 2 = 0
n = 2, x = 4 – 6 + 2 = 0
n = 3, x = 9 – 9 + 2 = 2
n = 4, x = 16 – 12 + 2 = 6
n = 5, x = 25 – 15 + 2 = 12
n = 6, x = 36 – 18 + 2 = 20
Incorrect
We see that each number in the given set follow the relation x = n2 – 3n + 2 as for
n = 1, x = 1 – 3 + 2 = 0
n = 2, x = 4 – 6 + 2 = 0
n = 3, x = 9 – 9 + 2 = 2
n = 4, x = 16 – 12 + 2 = 6
n = 5, x = 25 – 15 + 2 = 12
n = 6, x = 36 – 18 + 2 = 20
-
Question 14 of 20
14. Question
The set equivalent to the set {1, 2, 3, 4, 5, 6} is
Correct
A set does not change if the order of the elements is changed.
Incorrect
A set does not change if the order of the elements is changed.
-
Question 15 of 20
15. Question
Let R = {(a, a)} be a relation on a set A, Then R is
Correct
Incorrect
-
Question 16 of 20
16. Question
The number of proper subsets of the set {1, 2, 3} is
Correct
Number of proper subsets = 23 – 2 = 6
Incorrect
Number of proper subsets = 23 – 2 = 6
-
Question 17 of 20
17. Question
If A and B are two given sets, then A ∪ (A ∩ B) is equal to
Correct
A ∩ B ∩ A. Hence A ∪ (A ∩ B) = A
Incorrect
A ∩ B ∩ A. Hence A ∪ (A ∩ B) = A
-
Question 18 of 20
18. Question
If A = {x : x is an integer, x2< 1}, then the elements of ‘A’ are
Correct
If x2< 1 ⇒ –1 < x < 1 & x is an integer ∴ x ∈ {–1, 0, 1}
Incorrect
If x2< 1 ⇒ –1 < x < 1 & x is an integer ∴ x ∈ {–1, 0, 1}
-
Question 19 of 20
19. Question
In a town of 10, 000 families it was found that 40% family buy newspaper A, 20% families buy newspaper B and 10% families buy newspaper C, 5% families by A and B, 3% buy B and C and 4% buy A and C. If 2%families buy all the three newspapers, then number of families which buy A only is
Correct
n(A) = 40% of 10000 = 4000
n(B) = 20% of 10, 000 = 2000
n(C) = 10% of 10, 000 = 1000
n(A ∩ B) = 5% of 10000 = 500
n(B ∩ C) = 3% of 10000 = 300
n(C ∩ A) = 4% of 10000 = 400
n(A ∩ B ∩ C ) = 2% of 10,000 = 200
We want to find n(A ∩ BC ∩ CC) = n[A ∩ (B ∩ C)C] = n(A) – n[A ∩ B ∪ C] = n(A) –n[(A ∩ B) ∪ (A ∩ C)]
= n(A) – [n(A ∩ B) + n(A ∩ C) – n(A ∩ B ∩ C)] = 4000 – [500 + 400 – 200] = 4000 – 700 = 3300
or
Incorrect
n(A) = 40% of 10000 = 4000
n(B) = 20% of 10, 000 = 2000
n(C) = 10% of 10, 000 = 1000
n(A ∩ B) = 5% of 10000 = 500
n(B ∩ C) = 3% of 10000 = 300
n(C ∩ A) = 4% of 10000 = 400
n(A ∩ B ∩ C ) = 2% of 10,000 = 200
We want to find n(A ∩ BC ∩ CC) = n[A ∩ (B ∩ C)C] = n(A) – n[A ∩ B ∪ C] = n(A) –n[(A ∩ B) ∪ (A ∩ C)]
= n(A) – [n(A ∩ B) + n(A ∩ C) – n(A ∩ B ∩ C)] = 4000 – [500 + 400 – 200] = 4000 – 700 = 3300
or
-
Question 20 of 20
20. Question
Let R be a relation on N defined by x + 2y = 8. The domain of R is
Correct
Incorrect