JEE Main Physics Gravitation Online Test
Finish Quiz
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
JEE Main Physics Gravitation Online Test. JEE Main Online Test for Physics Gravitation. JEE Main Full Online Quiz for Physics Gravitation. JEE Main Free Mock Test Paper 2021. JEE Main 2021 Free Online Practice Test, Take JEE Online Test for All Subjects. JEE Main Question and Answers for Physics Gravitation. In this test You may find JEE Main all subjects Questions with Answers. Check JEE Main Question and Answers in English. This mock Test is free for All Students. Mock Test Papers are very helpful for Exam Purpose, by using below Mock Test Paper you may Test your Study for Next Upcoming Exams. Now Scroll down below n Take JEE Main Physics Gravitation…
This paper has 20 questions.
Time allowed is 30 minutes.
The JEE Main Physics Gravitation is Very helpful for all students. Now Scroll down below n click on “Start Quiz” or “Start Test” and Test yourself.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
-
Question 1 of 20
1. Question
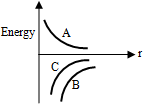
Figure shows the variation of energy with the orbit radius r of a satellite in a circular motion. Mark the correct statement.
Correct
Kinetic energy KE = GMm/2r
Potential energy PE = – GMm/r
And the total energy E = – GMm/2r
Kinetic energy is always positive and KE ∝ 1/r
Potential energy is negative and |PE| ∝ 1/r
Similarly total energy is also negative and |E| ∝ 1/r
Also |E| < |PE|
∴ A is kinetic energy, B is potential energy and C is total energy of the satellite.
Incorrect
Kinetic energy KE = GMm/2r
Potential energy PE = – GMm/r
And the total energy E = – GMm/2r
Kinetic energy is always positive and KE ∝ 1/r
Potential energy is negative and |PE| ∝ 1/r
Similarly total energy is also negative and |E| ∝ 1/r
Also |E| < |PE|
∴ A is kinetic energy, B is potential energy and C is total energy of the satellite.
-
Question 2 of 20
2. Question
A planet revolving around sun in an elliptical orbit has a constant
Correct
In elliptical orbit un is at one of the foci hence the distance between the planet and sun changes as planet revolves hence linear speed, kinetic energy and potential energy of planet do not remain constant
Incorrect
In elliptical orbit un is at one of the foci hence the distance between the planet and sun changes as planet revolves hence linear speed, kinetic energy and potential energy of planet do not remain constant
-
Question 3 of 20
3. Question
Both earth and moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon
Correct
Moon is revolving around earth in almost circular orbit. Sun exerts gravitational pull on both, earth and moon. When observed from sun, the orbit of the moon will not be strictly elliptical because they total gravitational force (i.e., force due to earth on moon and force due to sun on moon) is not central.
Incorrect
Moon is revolving around earth in almost circular orbit. Sun exerts gravitational pull on both, earth and moon. When observed from sun, the orbit of the moon will not be strictly elliptical because they total gravitational force (i.e., force due to earth on moon and force due to sun on moon) is not central.
-
Question 4 of 20
4. Question
Three particles each having a mass of 100 g are placed on the vertices of an equilateral triangle of side 20 cm. The work done in increasing the side of this triangle to 40 cm is
Correct
W = Uf – Ui
m = 0.1 kg, rf = 0.4 m and ri = 0.2 m
Substituting the value, we get
W = 5.0 × 10-12 J
Incorrect
W = Uf – Ui
m = 0.1 kg, rf = 0.4 m and ri = 0.2 m
Substituting the value, we get
W = 5.0 × 10-12 J
-
Question 5 of 20
5. Question
Two satellites S1 & S2 of equal masses revolve in the same sense around a heavy planet in coplanar circular orbit of radii R & 4R
Correct
Incorrect
-
Question 6 of 20
6. Question
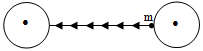
Two identical spherical masses are kept at some distance as shown. Potential energy when a mass m is taken from surface of one sphere to the other
Correct
Centre point is the unstable equilibrium position where potential energy is maximum.
Incorrect
Centre point is the unstable equilibrium position where potential energy is maximum.
-
Question 7 of 20
7. Question
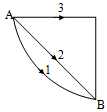
If W1, W2 and W3 represent the work done in moving a particle from A to B along three different paths 1, 2 and 3 respectively (as shown) in a gravitational field of point mass m then
Correct
Since the gravitational field is conservative field hence, the work done in taking a particle from one point to another in a gravitational field is path independent.
Incorrect
Since the gravitational field is conservative field hence, the work done in taking a particle from one point to another in a gravitational field is path independent.
-
Question 8 of 20
8. Question
Maximum height reached by a rocket fired with a speed equal to 50% of the escape velocity from earth’s surface is:
Correct
Applying energy conservation
⇒ R + h = 4h ⇒ h = R/3
Incorrect
Applying energy conservation
⇒ R + h = 4h ⇒ h = R/3
-
Question 9 of 20
9. Question
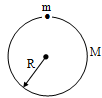
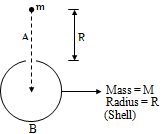
A thin spherical shell of mass M and radius R has a small hole. A particle of mass m is released at the mouth of the hole. Then
Correct
Net gravitational field inside a shell is zero. Hence, net force on the particle will be zero i.e., the particle stays at rest in its original position.
Incorrect
Net gravitational field inside a shell is zero. Hence, net force on the particle will be zero i.e., the particle stays at rest in its original position.
-
Question 10 of 20
10. Question
A satellite in a circular orbit of radius r has time period of 4 hrs. A satellite with orbital radius of 4r around the same planet will have a time period of:
Correct
Radius of orbit of the first satellite
R1 = R
Time period of the first satellite T = 4 hrs. and radius of orbit of second satellite = 4r The time period of satellite is given by
T2 = 8 × 4 = 32 hours.
Incorrect
Radius of orbit of the first satellite
R1 = R
Time period of the first satellite T = 4 hrs. and radius of orbit of second satellite = 4r The time period of satellite is given by
T2 = 8 × 4 = 32 hours.
-
Question 11 of 20
11. Question
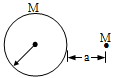
A particle of mass M is at a distance a from the surface of a thin spherical shell of equal mass and having radius a.
Correct
At centre, field is zero due to shell but non zero due to particle
∴ Ecentre = due to particle
Potential at centre is non zero due to both shell and particle.
Incorrect
At centre, field is zero due to shell but non zero due to particle
∴ Ecentre = due to particle
Potential at centre is non zero due to both shell and particle.
-
Question 12 of 20
12. Question
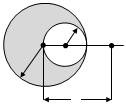
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at a distance 3R from the centre of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in the figure. The sphere with cavity now applies a gravitational force F2 on the same particle. The ratio F2/F1 is
Correct
From superposition principle, F1 = Fr + Fc
Here, Fr = force due to remaining part = F2
And Fc = force due to cavity
Incorrect
From superposition principle, F1 = Fr + Fc
Here, Fr = force due to remaining part = F2
And Fc = force due to cavity
-
Question 13 of 20
13. Question
If the distance between the earth And the sun were half its present value the number of days in a year would have been
Correct
T2 ∝ R3
Incorrect
T2 ∝ R3
-
Question 14 of 20
14. Question
A satellite orbits the earth at a height of 400 km above the surface. How much energy must be expended to rocket the satellite out of the earth’s gravitational influence? Mass of the satellite = 200 kg, mass of the earth = 6.0 × 1024 kg, radius of the earth = 6.4 × 106 m, G = 6.67 × 10-11 N-m2/kg2.
Correct
Given, height of the satellite above the earth’s surface (h) = 400 km = 0.4 × 106 m
Mass of the satellite (m) = 200 kg
Radius of earth (Re) = 6.4 × 106 m
Mass of earth (Me) = 6.0 × 1024 kg
Gravitational constant (G) = 6.67 × 10-11 N-m2/kg2
Energy required send a satellite out of earth’s gravitational influence is called its binding energy.
Binding energy of a satellite =
= 5.885 × 109 J
= 5.9 × 109 J
Incorrect
Given, height of the satellite above the earth’s surface (h) = 400 km = 0.4 × 106 m
Mass of the satellite (m) = 200 kg
Radius of earth (Re) = 6.4 × 106 m
Mass of earth (Me) = 6.0 × 1024 kg
Gravitational constant (G) = 6.67 × 10-11 N-m2/kg2
Energy required send a satellite out of earth’s gravitational influence is called its binding energy.
Binding energy of a satellite =
= 5.885 × 109 J
= 5.9 × 109 J
-
Question 15 of 20
15. Question
A particle of mass m is moved from A to B as shown in figure. Then potential energy of the particle
Correct
Outside the shell V0 =
Therefore, from A to surface v and hence the potential energy will decrease.
Inside the shell potential is constant. Hence, the potential energy is constant.
Incorrect
Outside the shell V0 =
Therefore, from A to surface v and hence the potential energy will decrease.
Inside the shell potential is constant. Hence, the potential energy is constant.
-
Question 16 of 20
16. Question
A satellite is in a circular orbit around the earth has kinetic energy Ek. Minimum amount of energy that is added so that it escapes the earth’s gravitational field is:
Correct
Total Mechanical energy (kinetic energy)
∴ TME = – Ek
For escape, TME = 0
i.e., If, Ek is provided then TME. Becomes Zero
Hence. The minimum amount of energy that is added so that it escapes the earth’s gravitational field is Ek.
Incorrect
Total Mechanical energy (kinetic energy)
∴ TME = – Ek
For escape, TME = 0
i.e., If, Ek is provided then TME. Becomes Zero
Hence. The minimum amount of energy that is added so that it escapes the earth’s gravitational field is Ek.
-
Question 17 of 20
17. Question
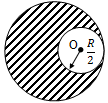
Assertion From a solid sphere of radius R, a hole of radius R/2 is cut as shown in figure. To find the magnitude of gravitational potential and gravitational field strength at O, we can directly subtract Potential due to hole (before removing) from potential due to whole sphere (before removing). The same can be done to find field strength at O, although potential is a scalar quantity and field strength is a vector quantity.
Reason In gravity, it is done like this. It makes no difference, whether the field strength is added/subtracted by vector method or by scalar method.
Correct
Incorrect
-
Question 18 of 20
18. Question
At a distance 320 km above the surface of earth, the value of acceleration due to gravity will be lower than its value on the surface of the earth by nearly (radius of earth = 6400 km)
Correct
Incorrect
-
Question 19 of 20
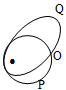
19. Question
Assertion A planet may orbit around a star either in orbit P or orbit Q. The speed of planet at O is same for both orbits.
Reason Planets orbit around a star with uniform velocity.
Correct
In circular path, star should lie at centre.
Incorrect
In circular path, star should lie at centre.
-
Question 20 of 20
20. Question
If the distance between the earth and the sun were half its present value, the number of days in a year would have been
Correct
From Kepler’s third law
T2 = 129 days
Incorrect
From Kepler’s third law
T2 = 129 days

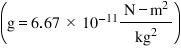
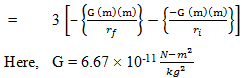

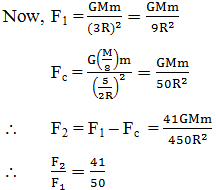
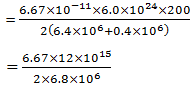
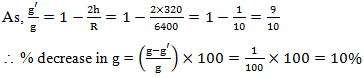
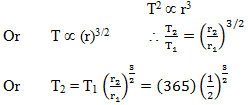
I know computer . help me anything work. Your solve the problem .I know computer
I know computer
computer is very use full in over life