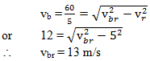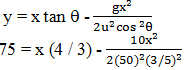JEE Main Physics Kinematics Online Test
Finish Quiz
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
JEE Main Physics Kinematics Online Test. JEE Main Online Test for Physics Kinematics. JEE Main Full Online Quiz for Physics Kinematics. JEE Main Free Mock Test Paper 2021. JEE Main 2021 Free Online Practice Test, Take JEE Online Test for All Subjects. JEE Main Question and Answers for Physics Kinematics. In this test You may find JEE Main all subjects Questions with Answers. Check JEE Main Question and Answers in English. This mock Test is free for All Students. Mock Test Papers are very helpful for Exam Purpose, by using below Mock Test Paper you may Test your Study for Next Upcoming Exams. Now Scroll down below n Take JEE Main Physics Kinematics…
This paper has 20 questions.
Time allowed is 30 minutes.
The JEE Main Physics Kinematics is Very helpful for all students. Now Scroll down below n click on “Start Quiz” or “Start Test” and Test yourself.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
-
Question 1 of 20
1. Question
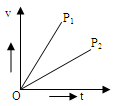
Shown in the figure are the velocity time graphs of the two particles P1 and P2 moving in same straight line in same direction. Which of the following statements about their relative motion is true?
Their relative velocity
Correct
a = slope of v-t graph.
a1 > a2
vr = v1 – v2 = a1t – a2t = (a1 – a2)t
∴ vr ∝ t
Incorrect
a = slope of v-t graph.
a1 > a2
vr = v1 – v2 = a1t – a2t = (a1 – a2)t
∴ vr ∝ t
-
Question 2 of 20
2. Question
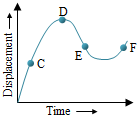
The displacement-time graph of a moving particle is shown below. The instantaneous velocity of the particle is negative at the point
Correct
Slope is negative at the point E.
Incorrect
Slope is negative at the point E.
-
Question 3 of 20
3. Question
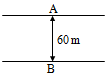
A man is crossing a river flowing with velocity of 5 m/s. he reaches a point directly across at a distance of 60 m in 5 sec. his velocity in still water should be
Correct
Incorrect
-
Question 4 of 20
4. Question
A body starts from rest and is uniformly accelerated for 30s. the distance travelled in the first 10 s is x1, next 10 s is x2 and the last 10 s is x3.
Then, x1 ; x2 ; x3 is
Correct
x1 = 1/2 a(10)2 = 50a
x2 = 1/2 a(20)2 – 1/2 (a) (10)2 = 150a
x3 = 1/2 a(30)2 – 1/2 a (20)2 = 250a
∴ x1 : x2 : x3 = 1 : 3 : 5.
Incorrect
x1 = 1/2 a(10)2 = 50a
x2 = 1/2 a(20)2 – 1/2 (a) (10)2 = 150a
x3 = 1/2 a(30)2 – 1/2 a (20)2 = 250a
∴ x1 : x2 : x3 = 1 : 3 : 5.
-
Question 5 of 20
5. Question
Two cars start off to race with velocities 4 m/s and 2 m/s and travel in straight line with uniform accelerations 1 m/s2 and 2 m/s2 respectively. if they reach the final point at the same instant, then the length of the path is
Correct
s = 4t +1/2 (1)t2= 2t +1/2(2) t2
Or 4t + 0.5t2 = 2t + t2
Or = 2t or t = 0
And t = 4s
∴ s = (4) (4) + 1/2 (1) (4)2 = 16 + 8 = 24 m
Incorrect
s = 4t +1/2 (1)t2= 2t +1/2(2) t2
Or 4t + 0.5t2 = 2t + t2
Or = 2t or t = 0
And t = 4s
∴ s = (4) (4) + 1/2 (1) (4)2 = 16 + 8 = 24 m
-
Question 6 of 20
6. Question
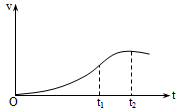
The velocity-time graph of a particle in one-dimensional motion is shown in figure. Which of the following formulae are correct for describing the motion of the particle over the time interval t1 to t2.
Correct
The slope of the given graph over the time interval t1 to t2 is not constant and is not uniform. It means acceleration is not constant and is not uniform, therefore relations (a), (b), (e) are not correct which is for uniform accelerated motion, but relations (c), (d) and (f) are correct, because these relation are true for both uniform or non-uniform accelerated motion.
Incorrect
The slope of the given graph over the time interval t1 to t2 is not constant and is not uniform. It means acceleration is not constant and is not uniform, therefore relations (a), (b), (e) are not correct which is for uniform accelerated motion, but relations (c), (d) and (f) are correct, because these relation are true for both uniform or non-uniform accelerated motion.
-
Question 7 of 20
7. Question
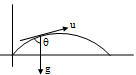
A ball projected upwards from the foot of a tower. The ball crosses the top of the tower twice after an interval of 6s and the ball reaches the ground after 12s. the height of the tower is (g = 10 m/s2)
Correct
tBC = 6/2 = 3s
tAC = 12/2 = 6s
∴ tAB = 3 s
∴ 0 = u – (10)6
or u = 60 m/s
Further h = utAB –1/2 gt2AB
= (60) (3) – 1/2 (10)(3)2 = 135 m
Incorrect
tBC = 6/2 = 3s
tAC = 12/2 = 6s
∴ tAB = 3 s
∴ 0 = u – (10)6
or u = 60 m/s
Further h = utAB –1/2 gt2AB
= (60) (3) – 1/2 (10)(3)2 = 135 m
-
Question 8 of 20
8. Question
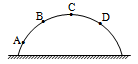
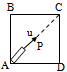
A stone is projected from ground. Its path is as shown in figure. At which point its speed is decreasing at fastest rate?
Correct
Rate of decrease of speed = g cos θ
q is minimum at A. therefore speed is decreasing at fastest rate at A.
Incorrect
Rate of decrease of speed = g cos θ
q is minimum at A. therefore speed is decreasing at fastest rate at A.
-
Question 9 of 20
9. Question
Ball A is dropped from the top of a building. At the same instant ball B is thrown vertically upwards from the ground. When the balls collide, they are moving in opposite directions and the speed of A is twice the speed of B. At what fraction of the height of the building did the collision occur?
Correct
Let h be the total height and x the desired fraction. Initial velocity of ball is u and at time of collision it is vB. Then,
Incorrect
Let h be the total height and x the desired fraction. Initial velocity of ball is u and at time of collision it is vB. Then,
-
Question 10 of 20
10. Question
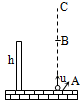
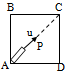
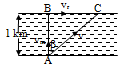
A large rectangular box moves vertically downward with an acceleration a. A toy gun fixed at A and aimed towards C fires a particle P.
Correct
(A) if a = g then relative acceleration to P will be zero. So path is straight line along PC.
(B) If a > g, then relative acceleration of P is upwards. therefore path of P with respect to box is as shown in figure.
So particle may hit AB or BC depending on the speed of P.
(C) If a < g, then relative acceleration of P is downwards. Therefore path of P with respect to box is as shown in figure.
So, the particle may hit CD or AD depending upon the speed of P.
Incorrect
(A) if a = g then relative acceleration to P will be zero. So path is straight line along PC.
(B) If a > g, then relative acceleration of P is upwards. therefore path of P with respect to box is as shown in figure.
So particle may hit AB or BC depending on the speed of P.
(C) If a < g, then relative acceleration of P is downwards. Therefore path of P with respect to box is as shown in figure.
So, the particle may hit CD or AD depending upon the speed of P.
-
Question 11 of 20
11. Question
A body released from great height falls freely towards the earth. Another body is released from the same height exactly one second later. The separation between the two bodies two second after the release of the second body is
Correct
As, ∆x = 1/2gt2 – 1/2 g (t – 1) 2
= 1/2 g [- (t – 1)2] = 1/2 g (2t – 1)
= 1/2 × 9.8× 5 m = 24.5 m
Incorrect
As, ∆x = 1/2gt2 – 1/2 g (t – 1) 2
= 1/2 g [- (t – 1)2] = 1/2 g (2t – 1)
= 1/2 × 9.8× 5 m = 24.5 m
-
Question 12 of 20
12. Question
A 120 m long train is moving in a direction with speed 20 m/s. a train moving with 30 m/s in the opposite direction and 130 m long crosses the first train in a time.
Correct
Total distance = 130 + 120 = 250 m
Relative velocity = 30 – (- 20) = 50 m/s
Here, 250/50 = 5 s
Incorrect
Total distance = 130 + 120 = 250 m
Relative velocity = 30 – (- 20) = 50 m/s
Here, 250/50 = 5 s
-
Question 13 of 20
13. Question
Rain drops fall vertically at a speed of 20 ms-1. At what angle do they fall on the wind screen of a car moving with a velocity of 15 ms-1, if the wind screen velocity inclined at an angle of 23º to the vertical?
Correct
Let the required angle is q.
tan (900 – θ) = 20/15
∴ cot θ = 20/15 = 4/3
⇒ θ = 370
∴ θ = 370 + 230 = 600
Incorrect
Let the required angle is q.
tan (900 – θ) = 20/15
∴ cot θ = 20/15 = 4/3
⇒ θ = 370
∴ θ = 370 + 230 = 600
-
Question 14 of 20
14. Question
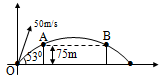
At t = 0 projectile is fired from a point O (taken as origin) on the ground with a speed of 50 m/s at an angle of 530 with the horizontal. it just passes two points A and B each at height 75 m above horizontal.
The horizontal separation between the points A and B is
Correct
Solving this equation we get.
x1 = 90m and x2 = 150 m
∴ AB = x2 – x1 = 60 m
Incorrect
Solving this equation we get.
x1 = 90m and x2 = 150 m
∴ AB = x2 – x1 = 60 m
-
Question 15 of 20
15. Question
The distance between two particles moving towards each other is decreasing at the rate of 6 m/s. if these particle travel with same speed and in the same direction then the separation increase at the rate of 4 m/s. the particles have speed as
Correct
when two particles moves towards each other, then v1 + v2 = 6 … (i)
When these particles moves in the same direction, then v1 – v2 = 4 … (ii)
By solving Eqs. (i) and (ii), we get v1 = 5 and v2 = 1 m/s
Incorrect
when two particles moves towards each other, then v1 + v2 = 6 … (i)
When these particles moves in the same direction, then v1 – v2 = 4 … (ii)
By solving Eqs. (i) and (ii), we get v1 = 5 and v2 = 1 m/s
-
Question 16 of 20
16. Question
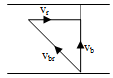
A man can swim with a speed of 4 km/h in still water. How long does he take to cross a river 1 km wide, if the river flows steadily 3 km/h and he makes his strokes normal to the river current. How far down the river does he go when he reaches the other bank?
Correct
Given, speed of man (vm) = 4 km/h
Speed of river (vr) = 3 km/h
Width of the river (d) = 1 km
Time taken by the man to cross the river
distance travelled along the river = vr × t = 3 ×1/4 = 3/4km = 3000/4 = 750 m
Incorrect
Given, speed of man (vm) = 4 km/h
Speed of river (vr) = 3 km/h
Width of the river (d) = 1 km
Time taken by the man to cross the river
distance travelled along the river = vr × t = 3 ×1/4 = 3/4km = 3000/4 = 750 m
-
Question 17 of 20
17. Question
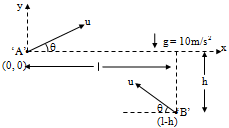
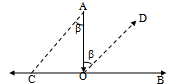
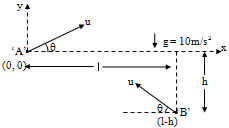
Two particles ‘A’ and ‘B’ are projected in a vertical plane with initial velocities having same magnitude u from points (0, 0) and (l, – h) at t = 0. The x-axis is horizontal and y-axis is vertical as shown.
The path of particle ‘A’ with respect to particle ‘B’ will be
Correct
Accelerations of both are same. Therefore relative acceleration between two is zero.
Further, vertical components of velocities of both are also same. Therefore, relative velocity in vertical direction is also zero.
Hence, the relative motion of A with respect to B is a straight line parallel to x-axis.
Incorrect
Accelerations of both are same. Therefore relative acceleration between two is zero.
Further, vertical components of velocities of both are also same. Therefore, relative velocity in vertical direction is also zero.
Hence, the relative motion of A with respect to B is a straight line parallel to x-axis.
-
Question 18 of 20
18. Question
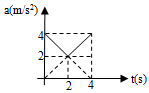
Starting from rest a particle moves in a straight line with acceleration a = {2 + |t – 2|} m/s2. Velocity of particle at the end of 4 s will be
Correct
Acceleration can be written as
a = 2 + 2 – t
or a = 4 – t for t < 2 s
and a = 2 + t – 2 or at = t for t > 2 s
therefore acceleration – time graph of the particle will be as shown below
Now since, dv = a dt
vf – vi = area under a-t graph
or vf – 0 = (4 × 4) – 1/2 (4)(2) = 12 m/s
or velocity of particle at the end of 4 s is 12 m/s.
Incorrect
Acceleration can be written as
a = 2 + 2 – t
or a = 4 – t for t < 2 s
and a = 2 + t – 2 or at = t for t > 2 s
therefore acceleration – time graph of the particle will be as shown below
Now since, dv = a dt
vf – vi = area under a-t graph
or vf – 0 = (4 × 4) – 1/2 (4)(2) = 12 m/s
or velocity of particle at the end of 4 s is 12 m/s.
-
Question 19 of 20
19. Question
In projectile motion, the modulus of rate of change of speed
Correct
|Rate of change of speed| = g cos θ
| cos θ | first decrease then increases.
Incorrect
|Rate of change of speed| = g cos θ
| cos θ | first decrease then increases.
-
Question 20 of 20
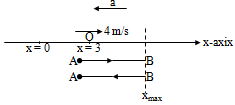
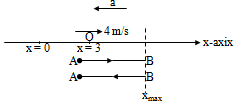
20. Question
A particle is moving along x-axis with constant acceleration. At t = 0, the particle is at x = 3 m and dx/dt m/s. The maximum value of x co-ordinate of the particle is observed 2 second later. Starting from t = 0 sec, after what time particle reaches its initial position again?
Correct
tAB = tBA = 2 second.
Therefore total time is, 2 + 2 = 4 s.
Incorrect
tAB = tBA = 2 second.
Therefore total time is, 2 + 2 = 4 s.