JEE Main Physics Rotational Motion Online Test
Finish Quiz
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
JEE Main Physics Rotational Motion Online Test. JEE Main Online Test for Physics Rotational Motion. JEE Main Full Online Quiz for Physics Rotational Motion. JEE Main Free Mock Test Paper 2021. JEE Main 2021 Free Online Practice Test, Take JEE Online Test for All Subjects. JEE Main Question and Answers for Physics Rotational Motion. In this test You may find JEE Main all subjects Questions with Answers. Check JEE Main Question and Answers in English. This mock Test is free for All Students. Mock Test Papers are very helpful for Exam Purpose, by using below Mock Test Paper you may Test your Study for Next Upcoming Exams. Now Scroll down below n Take JEE Main Physics Rotational Motion…
This paper has 20 questions.
Time allowed is 30 minutes.
The JEE Main Physics Rotational Motion is Very helpful for all students. Now Scroll down below n click on “Start Quiz” or “Start Test” and Test yourself.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
-
Question 1 of 20
1. Question
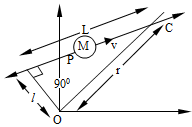
A particle of mass M moves along the line PC with velocity υ as shown. What is the angular momentum of the particle about O?
Correct
Angular momentum
= linear momentum × perpendicular distance of line of action of linear momentum from the axis of rotation = mv × l
Incorrect
Angular momentum
= linear momentum × perpendicular distance of line of action of linear momentum from the axis of rotation = mv × l
-
Question 2 of 20
2. Question
A force of 100 N is applied perpendicularly to the left edge of the rectangle as shown in figure. The torque (magnitude and direction) produced by this force with respect to an axis perpendicular to the plane of the rectangle at corner A and with respect to a similar axis at corner B are respectively.
Correct
As torque = force ´ perpendicular distance
∴ τA = 100 × 0.75 = 75 Nm counter clockwise,
τB = 100 × 1.25 = 125 Nm clockwise
Incorrect
As torque = force ´ perpendicular distance
∴ τA = 100 × 0.75 = 75 Nm counter clockwise,
τB = 100 × 1.25 = 125 Nm clockwise
-
Question 3 of 20
3. Question
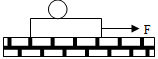
A plank with a uniform sphere placed on it resting on a smooth horizontal plane. Plank is pulled to right by a constant force F. If sphere does not slip over the plank. Which of the following is incorrect?
Correct
Incorrect
-
Question 4 of 20
4. Question
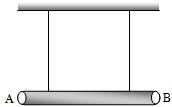
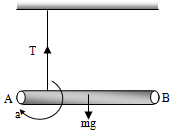
A uniform rod of mass m and length l is suspended by means of two light in extensible strings as shown in figure. Tension in one string immediately after the other string is cut is
Correct
When one string is cut off, the rod will rotate about the other point A. let a be the linear acceleration of centre of mass of the rod and a be the angular acceleration of the rod about A. As a figure.
Incorrect
When one string is cut off, the rod will rotate about the other point A. let a be the linear acceleration of centre of mass of the rod and a be the angular acceleration of the rod about A. As a figure.
-
Question 5 of 20
5. Question
A solid sphere rolls down two different inclined planes of same height but of different inclination. In both cases
Correct
In pure rolling, mechanical energy remains conserved therefore speed will be same in both the cases. Acceleration of the sphere down the plane
α ∝ sin θ
i.e., acceleration and hence, time of descend will be different.
Incorrect
In pure rolling, mechanical energy remains conserved therefore speed will be same in both the cases. Acceleration of the sphere down the plane
α ∝ sin θ
i.e., acceleration and hence, time of descend will be different.
-
Question 6 of 20
6. Question
An inclined plane makes an angle of 300 with horizontal. A solid sphere rolling down the inclined plane from rest without slipping has a linear acceleration equal to
Correct
(R = Radius of sphere)
Incorrect
(R = Radius of sphere)
-
Question 7 of 20
7. Question
A solid sphere, a ring and a disc all having same mass and radius are placed at the top of an incline and released. The friction coefficient between the objects and the incline are same but not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by
Correct
Friction is not sufficient for pure rolling. Therefore, maximum friction will act upwards in all the three bodies. So, linear acceleration of all the three bodies will be same and equal to (g sin θ – μg cos θ). Therefore, time taken by all the three will be same.
Incorrect
Friction is not sufficient for pure rolling. Therefore, maximum friction will act upwards in all the three bodies. So, linear acceleration of all the three bodies will be same and equal to (g sin θ – μg cos θ). Therefore, time taken by all the three will be same.
-
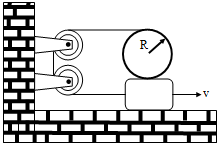
Question 8 of 20
8. Question
In the figure shown, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip then:
Correct
Incorrect
-
Question 9 of 20
9. Question
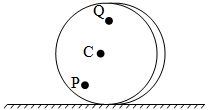
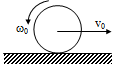
A uniform sphere of radius R is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The sphere comes to rest after moving some distance to the right. It follows that:
Correct
Incorrect
-
Question 10 of 20
10. Question
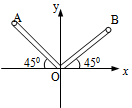
Two rods OA and OB of equal length and mass are lying on xy plane as shown in figure. Let lx, ly and lz be the moment of inertia of both the rods about x, y and z axis respectively. Then
Correct
Hence lx = ly < lz
Note: for lx and ly you can remember the following formula which is obtained by integration
Incorrect
Hence lx = ly < lz
Note: for lx and ly you can remember the following formula which is obtained by integration
-
Question 11 of 20
11. Question
A uniform ring of mass m and radius R is released from top of an inclined plane. The plane makes and angleθ with horizontal. The coefficient of friction between the ring and the plane is μ. Initially, the point of contact of ring and place is P. Angular momentum of the ring about an axis passing from point P and perpendicular to plane of motion as a function of time t is
Correct
Force of friction passes through point P. Hence, its torque about P will be zero. Only (mg sin θ) will have torque about P.
Thus, τ.t = ∆L
Or (mgR sinθ)t = L
Incorrect
Force of friction passes through point P. Hence, its torque about P will be zero. Only (mg sin θ) will have torque about P.
Thus, τ.t = ∆L
Or (mgR sinθ)t = L
-
Question 12 of 20
12. Question
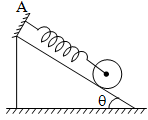
A uniform cylinder of mass M and radius R rolls without slipping down a slope of angle θ with horizontal. The cylinder is connected to a spring of force constant k at the centre, the other side of which is connected to a fixed support at A. The cylinder is released when the spring is unscratched. The force of friction (f) is
Correct
Initially the spring force kx is less than mg sin θ. i.e., the cylinder is accelerated downward or force of friction f is upwards. It will reverse its direction when kx > mg sin θ.
Incorrect
Initially the spring force kx is less than mg sin θ. i.e., the cylinder is accelerated downward or force of friction f is upwards. It will reverse its direction when kx > mg sin θ.
-
Question 13 of 20
13. Question
A disc is rolling (without slipping) on a horizontal surface C is its centre and Q and P are two points equidistance from C. Let vp, vq and vc be the magnitude of velocities of Point P, Q and C respectively, then
Correct
In case of pure rolling bottommost point is the instantaneous centre of zero.
Velocity.
Velocity of any pointy on the disc, v = rω, where r is the distance of point from O.
rQ > rC > rP
∴ vQ > vC > vP
Incorrect
In case of pure rolling bottommost point is the instantaneous centre of zero.
Velocity.
Velocity of any pointy on the disc, v = rω, where r is the distance of point from O.
rQ > rC > rP
∴ vQ > vC > vP
-
Question 14 of 20
14. Question
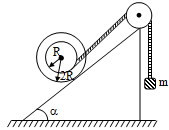
A spool of mass M and radius 2R lies on an inclined plane as shown in figure. A light thread is wound around the connecting tube of the spool and its free end carries a weight of mass m. the value of m so that system is in equilibrium is
Correct
Equilibrium of m gives
T = mg (T = Tension in string)
Net torque about point of contact of spool should be zero.
Hence,
(2R) (Mg sin α) = TR
Or 2Mg sin α = mg or m = 2M sin α
Incorrect
Equilibrium of m gives
T = mg (T = Tension in string)
Net torque about point of contact of spool should be zero.
Hence,
(2R) (Mg sin α) = TR
Or 2Mg sin α = mg or m = 2M sin α
-
Question 15 of 20
15. Question
A particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
Correct
Let the particle moves from A to A’ in time dt.
Incorrect
Let the particle moves from A to A’ in time dt.
-
Question 16 of 20
16. Question
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects, each of mass m, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity:
Correct
Incorrect
-
Question 17 of 20
17. Question
A cylinder rolls up an inclined plane, reaches some height and then rolls down (without slipping throughout these motions.) The directions of the frictional force acting on the cylinder are:
Correct
mg sin θ component is always down the plane whether it is rolling up or rolling down. Therefore, for no slipping, sense of angular acceleration should also be same in both the cases. Therefore, force of friction falways act upwards.
Incorrect
mg sin θ component is always down the plane whether it is rolling up or rolling down. Therefore, for no slipping, sense of angular acceleration should also be same in both the cases. Therefore, force of friction falways act upwards.
-
Question 18 of 20
18. Question
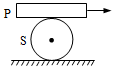
A plank P is placed on a solid cylinder S, which rolls on a horizontal surface. The two are of equal masses. There is no slipping at any of the surface in contact. The ratio of the kinetic energy of P to the kinetic energy of S is
Correct
Incorrect
-
Question 19 of 20
19. Question
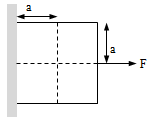
A horizontal force F is applied such that the block remains stationary, then which of the following statement is false?
Correct
As the block remains stationary therefore for translator equilibrium
∑fx = 0 ∴ f = N
And ∑ fy = 0 ∴ f = mg
For rotational equilibrium ∑ τ = 0
By taking the torque of different force about point O
τf + τf + τN + τmg = 0
As f and mg passing through point O
∴ τf + τN = 0
As τf ≠ 0
∴ τN ≠ 0 and torque by friction and normal reaction will be in opposite direction.
Incorrect
As the block remains stationary therefore for translator equilibrium
∑fx = 0 ∴ f = N
And ∑ fy = 0 ∴ f = mg
For rotational equilibrium ∑ τ = 0
By taking the torque of different force about point O
τf + τf + τN + τmg = 0
As f and mg passing through point O
∴ τf + τN = 0
As τf ≠ 0
∴ τN ≠ 0 and torque by friction and normal reaction will be in opposite direction.
-
Question 20 of 20
20. Question
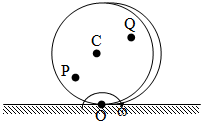
A uniform circular disc of radius r placed on a rough horizontal plane has initial velocity υ0 and an angular velocity ω0 as shown. The disc comes to rest after moving some distance in the direction of motion. Then
Correct
Incorrect


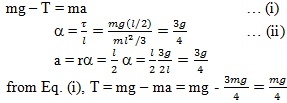
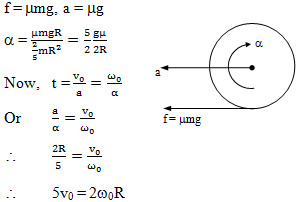
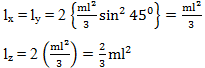
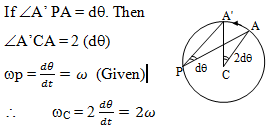
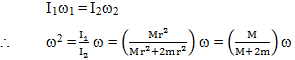
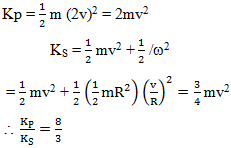
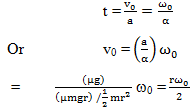
thanks a lot . nice work. helped me clear my concepts.